题目内容
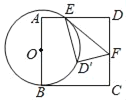
【题目】如图，四边形ABCD是矩形，点P是△ABD的内切圆的圆心，过P作PE⊥BC，PF⊥CD，垂足分别为点E、F，则四边形PECF和矩形ABCD的面积之比等于（ ）
A.1：2B.2：3C.3：4D.无法确定
【答案】A
【解析】
延长EP交AD于M，延长FP交AB于N，设AD＝a，AB＝b，BD＝c，⊙P的半径为r，利用平行线的性质得到PM⊥AD，PN⊥AB，再根据切线长定理得到PM＝PN＝r，根据直角三角形的内切圆半径的计算方法得到r＝
，所以PEPF＝
，利用完全平方公式和平方差公式得到PEPF＝
ab，然后计算四边形PECF和矩形ABCD的面积之比．
解：延长EP交AD于M，延长FP交AB于N，如图，设AD＝a，AB＝b，BD＝c，⊙P的半径为r，
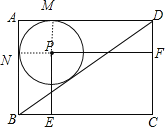
∵四边形ABCD是矩形，
∴AD∥BC，AB∥CD，
∵PE⊥BC，PF⊥CD，
∴PM⊥AD，PN⊥AB，
∵点P是△ABD的内切圆的圆心
∴PM＝PN＝r，
∴r＝，
∴PF＝a﹣＝
，PE＝b﹣＝
，
∴PEPF＝
＝
＝
，
而a2+b2＝c2，
∴PEPF＝
＝ab，
∴四边形PECF和矩形ABCD的面积之比＝ab：ab＝1：2．
故选：A．
练习册系列答案
相关题目
