Question

如图，在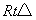ABC中，∠C＝90º，BD是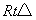ABC的一条角一平分线，点O、E、F分别在BD、BC、AC上，且四边形OECF是正方形，

（1）求证：点O在∠BAC的平分线上；

（2）若AC＝5，BC＝12，求OE的长

　　　　　　　　　　　　　　　　　

 

Answer 1

（1）过点O作ON⊥AB于点M

∵正方形OECF

∴OE＝EC＝CF＝OF，OE⊥BC于E，OF⊥AC于F

∵BD平分∠ABC，OM⊥AB于M，OE⊥BC于E

∴OM＝OE＝OF

∵OM⊥AB于M， OE⊥BC于E

∴∠AMO＝90°，∠AFO＝90°

∵

∴Rt△AMO≌Rt△AFO

∴∠MA0＝∠FAO

∴点O在∠BAC的平分线上

（2）方法一：

∵Rt△ABC中，∠C＝90°，AC＝5，BC＝12

∴AB＝13

易证：BE＝BM，AM＝AF

又BE＝BC－CE，AF＝：AC－CF，而CE＝CF＝OE

故：BE＝12－OE，AF＝5－OE

显然：BM＋AM＝AB

　即：BE＋AF＝13

12－OE＋5－OE＝13

解得OE＝2

方法二

利用面积法：

S△ABC＝

S△ABC＝

从而解得。