题目内容
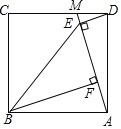
如图，点M是正方形ABCD边CD上一点，连接AM，作DE⊥AM于点E，BF⊥AM于点F，连接BE．
（1）求证：AE=BF；
（2）已知AF=2，四边形ABED的面积为24，求∠EBF的正弦值．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
新课标快乐提优暑假作业陕西旅游出版社系列答案暑假衔接培优教材浙江工商大学出版社系列答案欣语文化快乐暑假沈阳出版社系列答案
的值．
x+c与x轴交于点A和点B（1，0），与y轴交于点C（0，
），抛物线y1的顶点为G，GM⊥x轴于点M．将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2．
，把显示结果输入如图的程序中，则输出的结果是_____．
D. 
B. 
C. 
D. 
