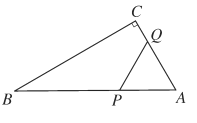
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点
,若点![]() 从点
从点![]() 出发以
出发以![]() /
/![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() /
/![]() 的速度向点
的速度向点![]() 运动,设
运动,设![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,运动的时间为
同时出发,运动的时间为![]() .
.
(1)求![]() 、
、![]() 的长(用含
的长(用含![]() 的式子表示).
的式子表示).
(2)当![]() 为何值时,
为何值时,![]() 是以
是以![]() 为底边的等腰三角形?
为底边的等腰三角形?
(3)当![]() 为何值时,
为何值时,![]() //
//![]() ?
?
【答案】(1)![]()
![]()
![]()
![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由题意,可知∠B=30°,AC=6cm.BP=2t,AP=ABBP,AQ=t;
(2)若△APQ是以PQ为底的等腰三角形,则有AP=AQ,即122t=t,求出t即可;
(3)先根据直角三角形的性质求出∠B的度数,再由平行线的性质得出∠QPA的度数,根据直角三角形的性质即可得出结论.
(1)∵![]() 中,
中,![]() ,
,![]()
![]() ,
,
∴![]() ,
,
又∵![]()
![]()
![]() ,
,
∴![]()
![]()
![]()
![]() cm,
cm,
由题意得:![]() ,
,![]()
则![]()
![]()
![]()
![]()
![]() ;
;
所以![]() cm,
cm,![]() cm
cm
(2)若![]() 是以
是以![]() 为底的等腰三角形,
为底的等腰三角形,
则有![]() ,即
,即![]()
![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 是以
是以![]() 为底边的等腰三角形.
为底边的等腰三角形.
(3)∵在![]() 中,
中,![]()
![]() ,
,![]()
![]()
![]() ,
,
∴![]()
![]() ,
,
若![]() //
//![]() ,
,
则有![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,解得:
,解得:![]() ,
,
故当![]() 时,
时,![]() //
//![]() .
.

练习册系列答案
相关题目