题目内容
 已知:如图,在⊙O中,弦AB∥CD.求证:弧AC与弧BD是等弧.
已知:如图,在⊙O中,弦AB∥CD.求证:弧AC与弧BD是等弧.考点:圆心角、弧、弦的关系
专题:证明题
分析:连结OA、OC、OD、OB,如图,由AB∥CD得到∠1=∠C,∠2=∠D,则∠1=∠2,再根据三角形外角性质得∠1=∠A+∠AOC,∠2=∠B+∠BOD,则∠AOC=∠BOD,然后根据圆心角、弧、弦的关系得到结论.
解答:证明:连结OA、OC、OD、OB,如图,
∵OC=OD,
∴∠1=∠2,
∵AB∥CD,
∴∠1=∠C,∠2=∠D,
∴∠1=∠2,
∵∠1=∠A+∠AOC,∠2=∠B+∠BOD,
而OA=OB,
∴∠A=∠B,
∴∠AOC=∠BOD,
∴弧AC与弧BD是等弧

∵OC=OD,
∴∠1=∠2,
∵AB∥CD,
∴∠1=∠C,∠2=∠D,
∴∠1=∠2,
∵∠1=∠A+∠AOC,∠2=∠B+∠BOD,
而OA=OB,
∴∠A=∠B,
∴∠AOC=∠BOD,
∴弧AC与弧BD是等弧
点评:本题考查了圆心角、弧、弦的关系:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
下列判断中,你认为正确的是( )
| A、-3的相反数是3 | ||
| B、-3的倒数是3 | ||
| C、(-1)2012=-1 | ||
D、
|
一条弧所对的圆心角为60°,那么这条弧所对的圆周角为( )
| A、30° | B、60° |
| C、120° | D、150° |
计算(ab)(3a2b2)3的结果是( )
| A、-3a3b3 |
| B、27a7b7 |
| C、-27a7b7 |
| D、-3a7b7 |
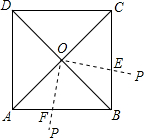 如图,正方形纸片ABCD对角线AC,BD交于点O,将一根木条的一端固定在点O处,此时木条与BC交于点E,将木条绕点O顺时针旋转90°,此时木条与AB交于点F
如图,正方形纸片ABCD对角线AC,BD交于点O,将一根木条的一端固定在点O处,此时木条与BC交于点E,将木条绕点O顺时针旋转90°,此时木条与AB交于点F 如图是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的表面积及全面积(结果保留π)
如图是一个立体图形的三视图,请写出这个立体图形的名称,并计算这个立体图形的表面积及全面积(结果保留π) 已知在△ABC中,AB=10,AC=9,BC=7,在△ADE中,AD=4,AE=
已知在△ABC中,AB=10,AC=9,BC=7,在△ADE中,AD=4,AE=