题目内容
已知方程组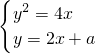 有两个实数解为
有两个实数解为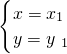 和
和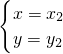 且x1x2≠0,x1≠x2,设
且x1x2≠0,x1≠x2,设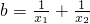 ,
,
(1)求a的取值范围;
(2)试用关于a的代数式表示出b;
(3)是否存在b=3的a的值?若存在,就求出所有这样的a的值;若不存在,请说明理由.
解:(1)∵y2=4x①,y=2x+a②,
把②代入①得
4x2+(4a-4)x+a2=0③,
又∵原方程组有两组实数解,且x1x2≠0,x1≠x2,
∴③就有两个不等的实数正根,
∴△=b2-4ac=(4a-4)2-4×4a2=-32a+16>0,
解得a< ,
,
由方程③可得
x1+x2=-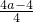 >0④,x1x2=
>0④,x1x2= >0⑤,
>0⑤,
解得a<1,a2>0(即a≠0),
∴a< 且a≠0;
且a≠0;
(2)∵b= +
+ =
=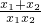 ,
,
把④⑤代入b中,得
b=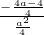 =
=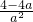 ⑥;
⑥;
(3)把b=3代入⑥得
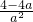 =3,
=3,
整理得3a2+4a-4=0,
解得a1=-2,a2= ,
,
由(1)中知a< 且a≠0;
且a≠0;
∴a=-2.
分析:(1)把y=2x+a代入y2=4x中,得到关于x的方程:4x2+(4a-4)x+a2=0③,又知原方程组有两组实数解,且x1x2≠0,x1≠x2,故此方程有不等的两实数正根,根据根的判别式可知△>0,结合方程③中根与系数的关系,可得x1+x2=-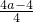 >0④,x1x2=
>0④,x1x2= >0⑤,三式联合可求出a的取值范围;
>0⑤,三式联合可求出a的取值范围;
(2)对b的右边进行,把④⑤代入,即可求⑥;
(3)把b=3代入⑥,解关于a的一元二次方程,结合(1)中a的取值范围,即可求a.
点评:本题综合考查了根的判别式和根与系数的关系,在解不等式时一定要注意数值的正负与不等号的变化关系.
把②代入①得
4x2+(4a-4)x+a2=0③,
又∵原方程组有两组实数解,且x1x2≠0,x1≠x2,
∴③就有两个不等的实数正根,
∴△=b2-4ac=(4a-4)2-4×4a2=-32a+16>0,
解得a<
 ,
,由方程③可得
x1+x2=-
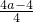 >0④,x1x2=
>0④,x1x2= >0⑤,
>0⑤,解得a<1,a2>0(即a≠0),
∴a<
 且a≠0;
且a≠0;(2)∵b=
 +
+ =
=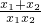 ,
,把④⑤代入b中,得
b=
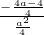 =
=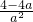 ⑥;
⑥;(3)把b=3代入⑥得
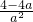 =3,
=3,整理得3a2+4a-4=0,
解得a1=-2,a2=
 ,
,由(1)中知a<
 且a≠0;
且a≠0;∴a=-2.
分析:(1)把y=2x+a代入y2=4x中,得到关于x的方程:4x2+(4a-4)x+a2=0③,又知原方程组有两组实数解,且x1x2≠0,x1≠x2,故此方程有不等的两实数正根,根据根的判别式可知△>0,结合方程③中根与系数的关系,可得x1+x2=-
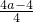 >0④,x1x2=
>0④,x1x2= >0⑤,三式联合可求出a的取值范围;
>0⑤,三式联合可求出a的取值范围;(2)对b的右边进行,把④⑤代入,即可求⑥;
(3)把b=3代入⑥,解关于a的一元二次方程,结合(1)中a的取值范围,即可求a.
点评:本题综合考查了根的判别式和根与系数的关系,在解不等式时一定要注意数值的正负与不等号的变化关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有两个实数解,且
有两个实数解,且 有两个实数解
有两个实数解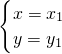 和
和 ,求m的值.
,求m的值. 有两个实数解
有两个实数解 和
和 ,且
,且 ,求m的值.
,求m的值. 有两个实数解
有两个实数解 和
和 ,且
,且 ,求m的值.
,求m的值.