题目内容
16.在平面直角坐标系xOy中,抛物线y=-x2+2mx-m2+1的对称轴是直线x=1.(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当-1<p<2时,点M关于y轴的对称点都在直线y=kx-4的上方,求k的取值范围.
分析 (1)由抛物线的对称轴方程可求得m=1,从而可求得抛物线的表达式;
(2)将x=3代入抛物线的解析式,可求得y2=3,将y=3代入抛物线的解析式可求得x1=-1,x2=3,由抛物线的开口向下,可知当当n<-1或n>3时,y1<y2;
(3)先根据题意画出点M关于y轴对称点M′的轨迹,然后根据点M关于y轴的对称点都在直线y=kx-4的上方,列出关于k的不等式组即可求得k的取值范围.
解答 解:(1)∵抛物线的对称轴为x=1,
∴x=-$\frac{b}{2a}$=-$\frac{2m}{-1×2}$=1.
解得:m=1.
∴抛物线的解析式为y=-x2+2x.
(2)将x=3代入抛物线的解析式得y=-32+2×3=-3.
将y=-3代入得:-x2+2x=-3.
解得:x1=-1,x2=3.
∵a=-1<0,
∴当n<-1或n>3时,y1<y2.
(3)设点M关于y轴对称点为M′,则点M′运动的轨迹如图所示: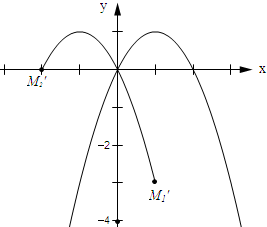
∵当P=-1时,q=-(-1)2+2×(-1)=-3.
∴点M关于y轴的对称点M1′的坐标为(1,-3).
∵当P=2时,q=-22+2×2=0,
∴点M关于y轴的对称点M2′的坐标为(-2,0).
①当k<0时,
∵点M关于y轴的对称点都在直线y=kx-4的上方,
∴-2k-4≤0.
解得:k≥-2.
②当k>0时,
∵点M关于y轴的对称点都在直线y=kx-4的上方,
∴k-4≤-3.
解得;k≤1.
∴k的取值范围是-2≤k≤1.
点评 本题主要考查的是二次函数的综合应用,解答本题需要同学们熟练掌握二次函数的图象和性质,利用数形结合思想列出关于k的不等式组是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
1. 如图,已知在△ABC中,D是边BC的中点,$\overrightarrow{BA}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,那么$\overrightarrow{DA}$等于( )
如图,已知在△ABC中,D是边BC的中点,$\overrightarrow{BA}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,那么$\overrightarrow{DA}$等于( )
 如图,已知在△ABC中,D是边BC的中点,$\overrightarrow{BA}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,那么$\overrightarrow{DA}$等于( )
如图,已知在△ABC中,D是边BC的中点,$\overrightarrow{BA}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,那么$\overrightarrow{DA}$等于( )| A. | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ | B. | $\overrightarrow a-\frac{1}{2}\overrightarrow b$ | C. | $\frac{1}{2}\overrightarrow b-\overrightarrow a$ | D. | $\overrightarrow b-\frac{1}{2}\overrightarrow a$ |
8.已知△ABC中,AB=6,BC=4,那么边AC的长可能是下列哪个值( )
| A. | 11 | B. | 5 | C. | 2 | D. | 1 |
 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上. 在空中,自地面算起,每升高1千米,气温下降若干度(℃).某地空中气温t(℃)与高度h(千米)间的函数的图象如图所示.观察图象可知:该地面高度h>4千米时,气温低于0℃.t关于h的函数解析式为t=-6h+24.
在空中,自地面算起,每升高1千米,气温下降若干度(℃).某地空中气温t(℃)与高度h(千米)间的函数的图象如图所示.观察图象可知:该地面高度h>4千米时,气温低于0℃.t关于h的函数解析式为t=-6h+24. 如图,延长线段AB至点C,使BC=$\frac{1}{2}$AB,反向延长AB至D,使AD=$\frac{1}{3}$AB.
如图,延长线段AB至点C,使BC=$\frac{1}{2}$AB,反向延长AB至D,使AD=$\frac{1}{3}$AB.