题目内容
【题目】如图，在四边形ABCD中，∠BAD=25°，∠ADC=115°，O为AB的中点，以点O为圆心、AO长为半径作圆，恰好点D在⊙O上，连接OD，若∠EAD=25°，下列说法中不正确的是（ ）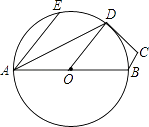 
A.D是劣弧 
的中点
B.CD是⊙O的切线
C.AE∥OD
D.∠DOB=∠EAD
【答案】D
【解析】解：A、∵∠BAD=25°，∠EAD=25°，
∴∠DAB=∠EAD，
∴ 
= 
，故此选项正确，不合题意；
B、∵∠BAD=25°，
∴∠ADO=25°，
∵∠ADC=115°，
∴∠ODC=90°，
∴CD是⊙O的切线，故此选项正确，不合题意；
C、∵∠EAD=∠ADO，
∴AE∥DO，故此选项正确，不合题意；
D、无法得出∠DOB=∠EAD，故此选项错误，符合题意．
故选：D．
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识，掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线．
练习册系列答案
名校课堂系列答案
相关题目
【题目】已知函数
，它的图象犹如老师的打钩，因此人们称它为对钩函数(的一支)．下表是
与
的几组对应值：
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
请你根据学习函数的经验，利用上述表格所反映出的与之间的变化规律，对该函数的图象与性质进行探究．
（1）如图，在平面直角坐标系
中，已描出了上表中各对对应值为坐标的点，请根据描出的点，画出该函数的图象；
（2）请根据图象写出该函数的一条性质： ．
（3）当
时，的取值范围为 ，则
的取值范围为 ．
