题目内容
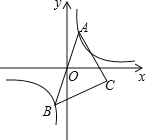
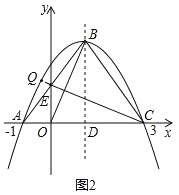
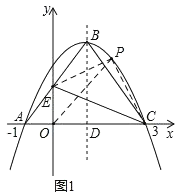
【题目】如图1,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0)、C(3,0),点B为抛物线顶点,直线BD为抛物线的对称轴,点D在x轴上,连接AB、BC,∠ABC=90°,AB与y轴交于点E,连接CE.

(1)求项点B的坐标并求出这条抛物线的解析式;
(2)点P为第一象限抛物线上一个动点,设△PEC的面积为S,点P的横坐标为m,求S关于m的函数关系武,并求出S的最大值;
(3)如图2,连接OB,抛物线上是否存在点Q,使直线QC与直线BC所夹锐角等于∠OBD,若存在请直接写出点Q的坐标;若不存在,说明理由.
【答案】(1)点B坐标为(1,2),y=﹣![]() x2+x+
x2+x+![]() ;(2)S=﹣
;(2)S=﹣![]() m2+2m+
m2+2m+![]() ,S最大值
,S最大值![]() ;(3)点Q的坐标为(﹣
;(3)点Q的坐标为(﹣![]() ,
,![]() ).
).
【解析】
(1)先求出抛物线的对称轴,证△ABC是等腰直角三角形,由三线合一定理及直角三角形的性质可求出BD的长,即可写出点B的坐标,由待定系数法可求出抛物线解析式;
(2)求出直线AB的解析式,点E的坐标,用含m的代数式表示出点P的坐标,如图1,连接EP,OP,CP,则由S△EPC=S△OEP+S△OCP﹣S△OCE即可求出S关于m的函数关系式,并可根据二次函数的性质写出S的最大值;
(3)先证△ODB∽△EBC,推出∠OBD=∠ECB,延长CE,交抛物线于点Q,则此时直线QC与直线BC所夹锐角等于∠OBD,求出直线CE的解析式,求出其与抛物线交点的坐标,即为点Q的坐标.
解:(1)∵A(﹣1,0)、C(3,0),
∴AC=4,抛物线对称轴为x=![]() =1,
=1,
∵BD是抛物线的对称轴,
∴D(1,0),
∵由抛物线的对称性可知BD垂直平分AC,
∴BA=BC,
又∵∠ABC=90°,
∴BD=![]() AC=2,
AC=2,
∴顶点B坐标为(1,2),
设抛物线的解析式为y=a(x﹣1)2+2,
将A(﹣1,0)代入,
得0=4a+2,
解得,a=﹣![]() ,
,
∴抛物线的解析式为:y=﹣![]() (x﹣1)2+2=﹣
(x﹣1)2+2=﹣![]() x2+x+
x2+x+![]() ;
;
(2)设直线AB的解析式为y=kx+b,
将A(﹣1,0),B(1,2)代入,
得![]() ,
,
解得,k=1,b=1,
∴yAB=x+1,
当x=0时,y=1,
∴E(0,1),
∵点P的横坐标为m,
∴点P的纵坐标为﹣![]() m2+m+
m2+m+![]() ,
,
如图1,连接EP,OP,CP,
则S△EPC=S△OEP+S△OCP﹣S△OCE
=![]() ×1×m+
×1×m+![]() ×3(﹣
×3(﹣![]() m2+m+
m2+m+![]() )﹣
)﹣![]() ×1×3
×1×3
=﹣![]() m2+2m+
m2+2m+![]() ,
,
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,根据二次函数和图象及性质知,当m=
<0,根据二次函数和图象及性质知,当m=![]() 时,S有最大值
时,S有最大值![]() ;
;
(3)由(2)知E(0,1),
又∵A(﹣1,0),
∴OA=OE=1,
∴△OAE是等腰直角三角形,
∴AE=![]() OA=
OA=![]() ,
,
又∵AB=BC=![]() AB=2
AB=2![]() ,
,
∴BE=AB﹣AE=![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵∠ODB=∠EBC=90°,
∴△ODB∽△EBC,
∴∠OBD=∠ECB,
延长CE,交抛物线于点Q,则此时直线QC与直线BC所夹锐角等于∠OBD,
设直线CE的解析式为y=mx+1,
将点C(3,0)代入,
得,3m+1=0,
∴m=﹣![]() ,
,
∴yCE=﹣![]() x+1,
x+1,
联立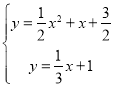 ,
,
解得,![]() 或
或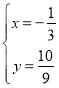 ,
,
∴点Q的坐标为(﹣![]() ,
,![]() ).
).

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;
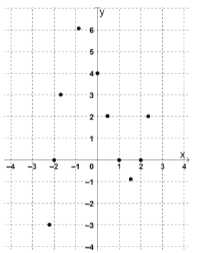
观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .