题目内容
5.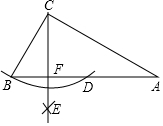 如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为( )
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=4,以点C为圆心,CB长为半径作弧,交AB于点D;再分别以点B和点D为圆心,大于$\frac{1}{2}$BD的长为半径作弧,两弧相交于点E,作射线CE交AB于点F,则AF的长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 连接CD,根据在△ABC中,∠ACB=90°,∠A=30°,BC=4可知AB=2BC=8,再由作法可知BC=CD=4,CE是线段BD的垂直平分线,故CD是斜边AB的中线,据此可得出BD的长,进而可得出结论.
解答  解:连接CD,
解:连接CD,
∵在△ABC中,∠ACB=90°,∠A=30°,BC=4,
∴AB=2BC=8.
∵作法可知BC=CD=4,CE是线段BD的垂直平分线,
∴CD是斜边AB的中线,
∴BD=AD=4,
∴BF=DF=2,
∴AF=AD+DF=4+2=6.
故选B.
点评 本题考查的是作图-基本作图,熟知线段垂直平分线的作法和直角三角形的性质是解答此题的关键.

练习册系列答案
相关题目
14.下列式子运算的结果为m2的是( )
| A. | m4•m -2 | B. | m6÷m3 | C. | (m-1)2 | D. | -m4÷(-m)2 |
 如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α(0°<α<180°),使点A仍在双曲线上,则α=30°.
如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α(0°<α<180°),使点A仍在双曲线上,则α=30°.