题目内容
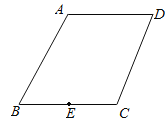
【题目】已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,作
上,作![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,交
,交![]() 延长线于
延长线于![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
【答案】![]()
【解析】
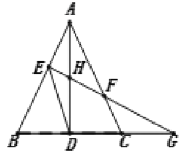
可证得A、E、D、G四点共圆,推出∠2=∠3,推出AF=FG,证得![]() ,得到HF=FC,AH=CG=2,再证得
,得到HF=FC,AH=CG=2,再证得![]() ,从而得到AH=CG=CD=DH=2,利用三角形中位线定理以及
,从而得到AH=CG=CD=DH=2,利用三角形中位线定理以及![]() ,可推出
,可推出![]() ,利用勾股定理求得AC的长,即可求解.
,利用勾股定理求得AC的长,即可求解.
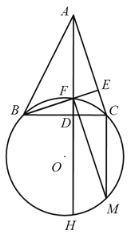
连接HC,AG,如图:
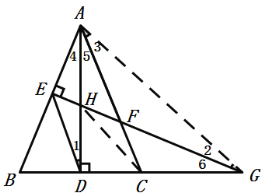
∵![]() ,
,![]() ,
,
∴∠AEG=∠ADG=90°,
∴A、E、D、G四点共圆,
∴∠1=∠2,
∵∠GFC=2∠1
∴∠GFC =2∠2,
又∵∠GFC=∠2+∠3,
∴∠2=∠3,
∴AF=FG,
∵![]() ,
,![]() ,
,
∴∠4=∠5,
∵∠4+∠B=90°,∠6+∠B=90°,
∴∠4=∠5=∠6,
在![]() 和
和![]() 中,
中,
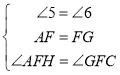 ,
,
∴![]() ,
,
∴HF=FC,AH=CG=2,
∵AF=FG,
∴AF+ FC=FG+ HF,
∴AC=GH,
在![]() 和
和![]() 中,
中,
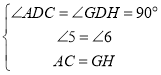 ,
,
∴![]() ,
,
∴CD=DH=2,
∴AH=CG=CD=DH=2,
∴点H为AD中点,点C为DG中点,
∴HC=![]() AG,HC∥AG,
AG,HC∥AG,
∴![]() ,
,
∴![]() ,由
,由![]() ,
,
∴![]() ,
,
在![]() 中,AD=AH+DH=4,DC=2,
中,AD=AH+DH=4,DC=2,
∴![]() ,
,
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目