题目内容
如图，PB是⊙O的切线，A是切点，D是
上一点，若∠BAC=70°，则∠ADC的度数是 度．
【答案】分析：设点E是优弧AC上的一点，由弦切角定理知，∠E=∠BAC=70°，再由圆内接四边形的对角互补知，∠D=180°-∠E=110°．
解答：
解：如图，∵在优弧AC上取点E，连接AE，CE，
PB是⊙O的切线，∠BAC=70°，
∴∠E=70°，
∴∠D=180°-∠E=110°．
点评：本题利用了弦切角定理和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
解答：
解：如图，∵在优弧AC上取点E，连接AE，CE，PB是⊙O的切线，∠BAC=70°，
∴∠E=70°，
∴∠D=180°-∠E=110°．
点评：本题利用了弦切角定理和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图，AB是⊙O的直径，P为AB延长线上任意一点，C为半圆ACB的中点，PD切⊙O于点D，连接CD交AB于点E．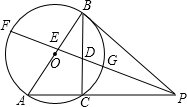
已知：如图，AB是⊙O的直径，PB切⊙O于点B，PA交⊙O于点C，∠A=60°，∠APB的平分线PF分别交BC、AB于点D、E，交⊙O于点F、G，且BD•AE=2
如图，BC是⊙O的直径，P是CB延长线上一点，PA切⊙O于点A，如果PA=| 3 |
| A、15° | B、30° |
| C、45° | D、60° |
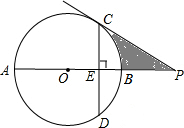如图，P是⊙O的直径AB延长线上的一点，PC切⊙O于点C，弦CD⊥AB，垂足为点E，若
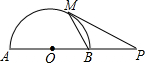如图，AB是⊙O的直径，点P在AB的延长线上，PM切⊙O于点M．若OA=a，PM=