题目内容
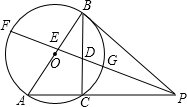 已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠A=60°,∠APB的平分线PF分别交BC、AB于点D、E,交⊙O于点F、G,且BD•AE=2
已知:如图,AB是⊙O的直径,PB切⊙O于点B,PA交⊙O于点C,∠A=60°,∠APB的平分线PF分别交BC、AB于点D、E,交⊙O于点F、G,且BD•AE=2| 3 |
(1)求证:△BPD∽△APE;
(2)求FE•EG的值;
(3)求tan∠BDE的值.
分析:(1)欲证△BPD∽△APE,必须找出角的等量关系,由PB是圆的切线,得出角∠PBC=∠A,再由PF是∠APB的平分线,得出∠APE=∠BPD,从而得出结论.
(2)由△BPD∽△APE得出角的等量关系,再由角相等得出边相等,然后由已知条件得出结论.
(3)由△BPD∽△APE得出对应边的比例关系,再由弦切角定理得出∠ABP=90°,再由角A的正弦值得出对应边的长度,再求tan∠BDE的值即可.
(2)由△BPD∽△APE得出角的等量关系,再由角相等得出边相等,然后由已知条件得出结论.
(3)由△BPD∽△APE得出对应边的比例关系,再由弦切角定理得出∠ABP=90°,再由角A的正弦值得出对应边的长度,再求tan∠BDE的值即可.
解答:(1)证明:∵BP切⊙O于点B,
∴∠PBC=∠A.
又∵PF为∠APB的角平分线,
∴∠APE=∠BPD.
∴△BPD∽△APE.
(2)解:∵△BPD∽△APE,
∴∠BDP=∠AEP.
∴∠BED=∠BDE.
∴BE=BD.
又∵BD•AE=2
,
∴BE•AE=2
.
∴FE•EG=BE•AE=2
.
(3)解:∵△BPD∽△APE,
∴
=
.
又∵AB是⊙O的直径,PB切⊙O于点B,
∴∠ABP=90°.
而∠A=60°,
∴sin∠A=sin60°=
=
,
∴
=
.
又BD=BE,
∴
=
.
又∵BE•AE=2
,
∴AE=2,BE=
.
∴AB=2+
,tan60°=
.
∴PB=2
+3.
∴tan∠BDE=tan∠BED=
=
=2+
.
∴∠PBC=∠A.
又∵PF为∠APB的角平分线,
∴∠APE=∠BPD.
∴△BPD∽△APE.
(2)解:∵△BPD∽△APE,
∴∠BDP=∠AEP.
∴∠BED=∠BDE.
∴BE=BD.
又∵BD•AE=2
| 3 |
∴BE•AE=2
| 3 |
∴FE•EG=BE•AE=2
| 3 |
(3)解:∵△BPD∽△APE,
∴
| BD |
| AE |
| PB |
| PA |
又∵AB是⊙O的直径,PB切⊙O于点B,
∴∠ABP=90°.
而∠A=60°,
∴sin∠A=sin60°=
| PB |
| PA |
| ||
| 2 |
∴
| BD |
| AE |
| ||
| 2 |
又BD=BE,
∴
| BE |
| AE |
| ||
| 2 |
又∵BE•AE=2
| 3 |
∴AE=2,BE=
| 3 |
∴AB=2+
| 3 |
| PB |
| AB |
∴PB=2
| 3 |
∴tan∠BDE=tan∠BED=
| BP |
| BE |
2
| ||
|
| 3 |
点评:本题主要考查,相似三角形的判定,弦切角定理以及角的正弦值、正切值的计算,难度适中.

练习册系列答案
相关题目
 22、已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.
22、已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC. (2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE.
(2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE. (1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.
(1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP. (2012•平谷区二模)已知,如图,AB是⊙O的直径,点E是
(2012•平谷区二模)已知,如图,AB是⊙O的直径,点E是
 已知:如图,AB是⊙O的直径,BC为⊙O的切线,过点B的弦BD⊥OC交⊙O于点D,垂足为E.
已知:如图,AB是⊙O的直径,BC为⊙O的切线,过点B的弦BD⊥OC交⊙O于点D,垂足为E.