题目内容
如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
(1)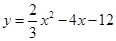 (2)①
(2)①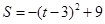 ,
,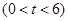 ②R坐标为(3,﹣18)
②R坐标为(3,﹣18)
解析试题分析:(1)设抛物线的解析式为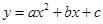 ,由题意知点A(0,﹣12),所以
,由题意知点A(0,﹣12),所以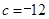 ,又
,又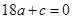 ,
,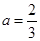 ,∵AB∥OC,且
,∵AB∥OC,且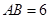 ,∴抛物线的对称轴是
,∴抛物线的对称轴是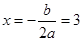 ,所以
,所以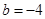 ,所以抛物线的解析式为
,所以抛物线的解析式为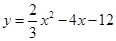
(2)①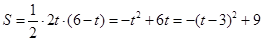 ,
,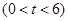
②当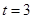 时,S取最大值为9.
时,S取最大值为9.
这时点P的坐标(3,﹣12),
点Q坐标(6,﹣6)
若以P、B、Q、R为顶点的四边形是平行四边形,有如下三种情况:
(Ⅰ)当点R在BQ的左边,且在PB下方时,点R的坐标(3,﹣18),将(3,﹣18)代入抛物线的解析式中,满足解析式,所以存在,点R的坐标就是(3,﹣18),
(Ⅱ)当点R在BQ的左边,且在PB上方时,点R的坐标(3,﹣6),将(3,﹣6)代入抛物线的解析式中,不满足解析式,所以点R不满足条件.
(Ⅲ)当点R在BQ的右边,且在PB上方时,点R的坐标(9,﹣6),将(9,﹣6)代入抛物线的解析式中,不满足解析式,所以点R不满足条件.
综上所述,点R坐标为(3,﹣18).
考点:函数与几何图形的结合
点评:作为试卷的最后一道题,难度稍大,中考试卷中,最后一题一般也都是压轴题,所以,做此类题目时,一般先做出第一问,本题第一问并不难。第二问需要分多钟情况进行讨论,最好排除掉一些错误的答案

 交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式.
交于点A,过点A分别作x轴、y轴的垂线,垂足为点B、C.如果四边形OBAC是正方形,求一次函数的关系式. 5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
5、如图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )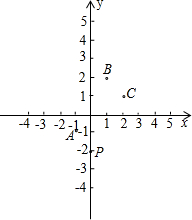 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次从点P跳到关于点A的对称点M处,第二次从点M跳到关于点B的对称点N处,第三次从点N跳到关于点C的对称点处,…如此下去. 如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为
如图所示,在平面直角坐标系xoy中,有一组对角线长分别为1,2,3的正方形A1B1C1O、A2B2C2B1、A3B3C3B2,其对角线OB1、B1B2、B2 B3依次放置在y轴上(相邻顶点重合),依上述排列方式,对角线长为n的第n个正方形的顶点An的坐标为 BE.
BE.