题目内容
①解方程: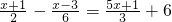
②解方程组: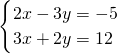 .
.
解:①去分母得,3(x+1)-(x-3)=2(5x+1)+36,
去括号得,3x+3-x+3=10x+2+36,
移项得,3x-x-10x=2+36-3-3,
合并同类项得,-8x=32,
系数化为1得,x=-4;
②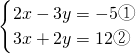 ,
,
①×2得,4x-6y=-10③,
②×3得,9x+6y=36④,
③+④得,13x=26,
解得x=2,
把x=2代入①得,4-3y=-5,
解得y=3,
所以,方程组的解是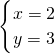 .
.
分析:①是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解;
②把第一个方程乘以2,第二个方程乘以3,然后利用加减消元法求解即可.
点评:①主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号;
②考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.
去括号得,3x+3-x+3=10x+2+36,
移项得,3x-x-10x=2+36-3-3,
合并同类项得,-8x=32,
系数化为1得,x=-4;
②
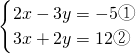 ,
,①×2得,4x-6y=-10③,
②×3得,9x+6y=36④,
③+④得,13x=26,
解得x=2,
把x=2代入①得,4-3y=-5,
解得y=3,
所以,方程组的解是
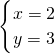 .
.分析:①是一个带分母的方程,所以要先去分母,再去括号,最后移项,合并同类项,系数化为1,从而得到方程的解;
②把第一个方程乘以2,第二个方程乘以3,然后利用加减消元法求解即可.
点评:①主要考查了解一元一次方程,注意在去分母时,方程两端同乘各分母的最小公倍数时,不要漏乘没有分母的项,同时要把分子(如果是一个多项式)作为一个整体加上括号;
②考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.

练习册系列答案
相关题目
数学应用题
(1)先完成下面的填空
学校团委组织65名团员为学校建花坛搬砖,初一同学每人搬6块砖,其他年级同学每人搬8块,总共搬了400块砖,问初一同学有多少人参加搬砖?
分析:设初一同学有x人参加搬砖,列表如下:
可列出方程: .
解得:x= ;
(2)仿照上题,写出下题的分析过程(可列表,可用语言表述,形式自选)
某市为更有效地利用水资源,制定了用水标准,如果一户三口之家每月用水量不超过M立方米,按每立方米1.30元收费;如果超过M立方米,超过部分按每立方米水2.90元收费,其余仍按每立方米1.30元计算.许清一家三人,1月份用水12立方米,支付水费22元,问该市制定的用水标准m是多少?许清一家超标使用了多少立方米的水?
分析:
列出方程组:
解得:
(1)先完成下面的填空
学校团委组织65名团员为学校建花坛搬砖,初一同学每人搬6块砖,其他年级同学每人搬8块,总共搬了400块砖,问初一同学有多少人参加搬砖?
分析:设初一同学有x人参加搬砖,列表如下:
| 参加年级 | 初一学生 | 其它年级学生 | 总数 |
| 参加人数 | x | 65 | |
| 每人搬砖 | 6 | 8 | - |
| 共搬砖 | 400 |
解得:x=
(2)仿照上题,写出下题的分析过程(可列表,可用语言表述,形式自选)
某市为更有效地利用水资源,制定了用水标准,如果一户三口之家每月用水量不超过M立方米,按每立方米1.30元收费;如果超过M立方米,超过部分按每立方米水2.90元收费,其余仍按每立方米1.30元计算.许清一家三人,1月份用水12立方米,支付水费22元,问该市制定的用水标准m是多少?许清一家超标使用了多少立方米的水?
分析:
列出方程组:
解得:
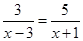
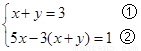
 或
或 或
或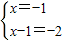 或
或