题目内容
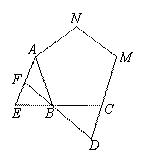
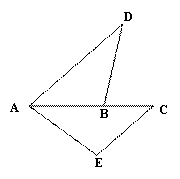
在平面直角坐标系xOy中,已知 A(-2,0),B(2,0),AC⊥AB于点A,AC=2,BD⊥AB于点B,BD=6,以AB为直径的半圆O上有一动点P(不与A、B两点重合),连接PD、PC,我们把由五条线段AB、BD、DP、PC、CA所组成的封闭图形ABDPC叫做点P的关联图形,如图1所示.
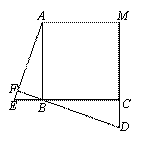
(1)如图2,当P运动到半圆O与y轴的交点位置时,求点P的关联图形的面积.
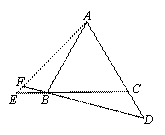
(2)如图3,连接CD、OC、OD,判断△OCD的形状,并加以证明.
(3)当点P运动到什么位置时,点P的关联图形的面积最大,简要说明理由,并求面积的最大值.
 | |||
 | |||
解:(1)∵A(-2,0),∴OA=2,
∵P是半圆O上的动点,P在y轴上,
 ∴OP=2, ∠AOP=90°,∵AC=2,∴四边形AOPC是正方形,
∴OP=2, ∠AOP=90°,∵AC=2,∴四边形AOPC是正方形,
∴正方形的面积是4,
又∵BD⊥AB,BD=6,
∴梯形OPDB的面积= ,
,
∴点P的关联图形的面积是12.
(2)判断△OCD是直角三角形.
证明:延长CP交BD于点F.则四边形ACFB为矩形,
∴CF=DF=4,∠DCF=45°,
又∵四边形AOPC是正方形,∴∠OCP=45°,
∴∠OCD=90°,∴OC⊥CD.
∴△OCD是直角三角形…
(3)连接OC交半圆O于点P,则点 P记为所确定的点的位置.
P记为所确定的点的位置.
理由如下:连接CD,梯形ACDB的面积= 为定值,
为定值,
要使点P的关联图形的面积最大,就要使△PCD的面积最小,∵CD为定长,∴P到CD的距离就要最小.
连接OC,设交半圆O于点P,∵AC⊥OA,AC=OA, ∴∠AOC=45°,过C作CF⊥BD于F,则ACFB为矩形,∴CF=DF=4, ∠DCF=45°,∴OC⊥CD,OC=2 ,∴PC在半圆外,设在半圆O上的任意一点P‘到CD的距离为P‘H,则P‘H+P‘O>OH>OC, ∵OC=PC+OP, ∴P′H> PC,
,∴PC在半圆外,设在半圆O上的任意一点P‘到CD的距离为P‘H,则P‘H+P‘O>OH>OC, ∵OC=PC+OP, ∴P′H> PC,
∴当点P运动到半圆O与OC的交点位置时,点P的关联图形的面积最大.
∵CD=4 ,CP=2
,CP=2 -2, ∴△PCD的面积=
-2, ∴△PCD的面积= ,
,
又∵梯形ACDB的面积= ,
,
∴点P的关联图形的最大面积是梯形ACDB的面积-△PCD的面积=16-(8-4 )=8+4
)=8+4 .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案为了解居民用水情况,晓娜在某小区随机抽查了10户家庭的月用水量,结果如下表:
| 月用水量(吨) | 5 | 6 | 7 | 8 | 9 | 10 |
| 户数 | 1 | 1 | 2 | 2 | 3 | 1 |
则这10户家庭的月用水量的平均数和众数分别是
A.7.8,9 B.7.8 ,3 C.4.5,9 D.4.5,3
,3 C.4.5,9 D.4.5,3
21.为了解南京市2012年市城镇非私营单位员工每月的收入状况,统计局对市城镇
非私营单位随机抽取了1000人进行抽样调查.整理样本数据,得到下列图表:
 |
市城镇非私营单位1000人月收入频数分布表
| 月工资x(元) | 频数(人) |
| x<2000 | 60 |
| 2000≤x<4000 | 610 |
| 4000≤x<6000 | 180 |
| 6000≤x<8000 | 50 |
| x≥8000 | 100 |
| 合计 | 1000 |
(1)如果1000人全部在金融行业抽取,这样的抽样是否合理?请说明理由;
(2)根据这样的调查结果,绘制条形统计图;
(3)2012年南京市城镇非私营单位月平均工资为5034元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
 B.
B.  C.
C.  D.
D. 
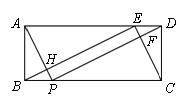

 图,正三角形ABC、正四边形ABCM、正五边形ABCMN中,点E在CB的延长线
图,正三角形ABC、正四边形ABCM、正五边形ABCMN中,点E在CB的延长线 AFB度数为 , 若将条件“正三角形、
AFB度数为 , 若将条件“正三角形、