题目内容
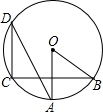如图，⊙O中，OA⊥BC，且∠AOB=50°，则∠ADC=分析：根据垂径定理得弧AC=弧AB，再根据同弧或等弧所对的圆周角等于它所对的圆心角的一半，得∠ADC=
∠AOB=25°．
| 1 |
| 2 |
解答：解：∵OA⊥BC，
∴弧AC=弧AB，
∴∠ADC=
∠AOB=25°．
∴弧AC=弧AB，
∴∠ADC=
| 1 |
| 2 |
点评：本题利用了垂径定理和圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
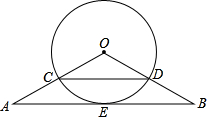如图，△OAB中，OA=OB，∠A=30°，⊙O经过AB的中点E分别交OA、OB于C、D两点，连接CD．
（2013•河北）如图，△OAB中，OA=OB=10，∠AOB=80°，以点O为圆心，6为半径的优弧
如图，⊙O中，OA⊥BC，∠CDA=35°，求∠AOB的度数．
如图，△AOB中，OA=OB=10，∠AOB=120°，以O为圆心，5为半径的⊙O与OA、OB相交．
如图，△AOB中，OA=OB，∠AOB=90゜，AD平分∠OAB交OB于D，OE⊥AD交AB于E，垂足为F，