题目内容
设x+2z=3y，试判断x2-9y2+4z2+4xz的值是不是定值，如果是定值，求出它的值．
考点：因式分解-运用公式法
专题：计算题
分析：原式结合后，利用完全平方公式及平方差公式变形，即可做出判断．
解答：解：x2-9y2+4z2+4xz=（x2+4z2+4xz）-9y2=（x+2z）2-（3y）2=（x+2z+3y）（x+2z-3y），
把x+2z=3y代入得：原式=6y•0=0，其值为定值．
把x+2z=3y代入得：原式=6y•0=0，其值为定值．
点评：此题考查了因式分解-运用公式法，熟练掌握完全平方公式及平方差公式是解本题的关键．
练习册系列答案
相关题目
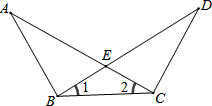已知：如图AC与BD相交于点E，∠1=∠2，∠A=∠D．则EA=ED，请说明理由．
比较图中各条线段的长短，并用刻度尺或圆规验证你的结论．