题目内容
20.先化简再求值:$\frac{{x}^{2}+x}{x-1}$÷$\frac{2x+2}{{x}^{2}-2x+1}$,其中x是方程x2-x-4=0的根.分析 先根据分式混合运算的法则把原式进行化简,再根据x2-x-4=0得出x2-x=4,代入原式进行计算即可.
解答 解:原式=$\frac{x(x+1)}{x-1}$÷$\frac{2(x+1)}{(x-1)^{2}}$
=$\frac{x(x+1)}{x-1}$•$\frac{(x-1)^{2}}{2(x+1)}$
=$\frac{{x}^{2}-x}{2}$,
∵x2-x-4=0,
∴x2-x=4,
∴原式=$\frac{4}{2}$=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$,则$\frac{a+b}{b+c}$的值为( )
| A. | $\frac{7}{9}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{8}{7}$ |
15.计算$\sqrt{48}-3\sqrt{\frac{1}{3}}$的结果是( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $-3\sqrt{3}$ | D. | $3\sqrt{3}$ |
5.一个两位数,个位数字为a,十为数字为b,则这个两位数为( )
| A. | ab | B. | ba | C. | 10a+b | D. | 10b+a |
10.在数7,0,-(-3),π中,正数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
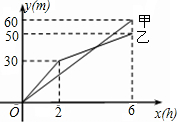 甲、乙两个工程队分别同时开始挖两段河渠,所挖河渠的长度与挖掘时间之间的关系如图所示,请根据图象所提供的信息解答下列问题:
甲、乙两个工程队分别同时开始挖两段河渠,所挖河渠的长度与挖掘时间之间的关系如图所示,请根据图象所提供的信息解答下列问题: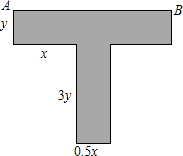 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求: