题目内容
已知二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),且与x轴交于A、B两点.
(1)试确定此二次函数的解析式;
(2)判断点P(﹣2,3)是否在这个二次函数的图象上?如果在,请求出△PAB的面积;如果不在,试说明理由.
考点: 待定系数法求二次函数解析式;二次函数图象上点的坐标特征.
分析: (1)已知了二次函数图象上的三点坐标,即可用待定系数法求出抛物线的解析式;
(2)将P点坐标代入二次函数的解析式中进行验证,即可得到P点是否在此函数图象上的结论;
令抛物线解析式的y=0,即可求得抛物线与x轴交点A、B的坐标,也就得到了AB的长;以AB为底,P点纵坐标的绝对值为高即可求得△PAB的面积.
解答: 解:(1)设二次函数的解析式为y=ax2+bx+c;
∵二次函数的图象经过点(0,3),(﹣3,0),(2,﹣5),则有:
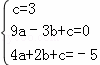 ,
,
解得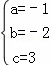 ;
;
∴y=﹣x2﹣2x+3.
(2)∵﹣(﹣2)2﹣2×(﹣2)+3=﹣4+4+3=3,
∴点P(﹣2,3)在这个二次函数的图象上,
∵﹣x2﹣2x+3=0,
∴x1=﹣3,x2=1;
∴与x轴的交点为:(﹣3,0),(1,0),
∴S△PAB=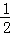 ×4×3=6.
×4×3=6.
点评: 此题主要考查了二次函数解析式的确定及图形面积的求法.

练习册系列答案
相关题目
 )2+(﹣1)101﹣0.25+(
)2+(﹣1)101﹣0.25+( )2÷(﹣
)2÷(﹣ )5÷|﹣8|
)5÷|﹣8| 的图象大致如图.若y1<y2,则自变量x的取值范围是( )
的图象大致如图.若y1<y2,则自变量x的取值范围是( )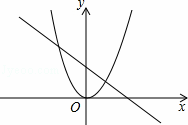
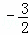 <x<2 B. x>2或x<
<x<2 B. x>2或x<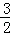 D. x<﹣2或x>
D. x<﹣2或x>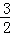

 ,1中,最小的实数是( )
,1中,最小的实数是( ) .﹣
.﹣ ,AB的长为( )
,AB的长为( ) B.8 C.4
B.8 C.4 D.4
D.4
 B.
B.  C.
C.  D.
D. 
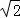 ≈1.414,
≈1.414,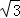 ≈1.732)
≈1.732)