题目内容
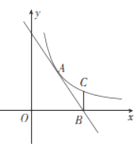
【题目】如图，反比例函数y=
(x>0)与直线AB交于点A(2，3)，直线AB与x轴交于点B(4，0)，过点B作x轴的垂线BC交反比例函数的图象于点C，在平面内有点D，使得以A，B，C，D四点为顶点的四边形为平行四边形，则平行四边形ABCD的面积为____________．
【答案】3
【解析】
先将A点的坐标代入反比例函数求得k的值，然后将x=4代入反比例函数解析式求得相应的y的值，即得点C的坐标；然后结合图象分类讨论以A、B、C、D为顶点的平行四边形，如图所示，找出满足题意的D的坐标，分三种情形求出平行四边形ABCD的面积即可.
把点A（2，3）代入y=
（x＞0）得：k=xy=6，
故该反比例函数解析式为：y=
．
∵点B（4，0），BC⊥x轴，
∴把x=4代入反比例函数y=，得
y=
．
则C（4，）．
①如图，当四边形ACBD为平行四边形时，AD∥BC且AD=BC．
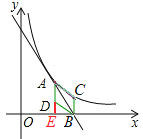
∵A（2，3）、B（4，0）、C（4，），
∴点D的横坐标为2，yA-yD=yC-yB，故yD=．
所以D（2，）,
延长AD交x轴于点E，则，
平行四边形ABCD的面积=梯形AEBC的面积-三角形DBE的面积
=
=3；
②如图，当四边形ABCD′为平行四边形时，AD′∥CB且AD′=CB．
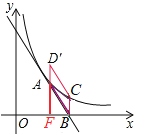
∵A（2，3）、B（4，0）、C（4，），
∴点D′的横坐标为2，yD′-yA=yC-yB，故yD′=
．
所以D′（2，）,
平行四边形ABCD′的面积=梯形AFBC的面积-三角形ABF的面积
=
=6-3
=3;
③如图，当四边形ABD″C为平行四边形时，AC=BD″且AC∥BD″．
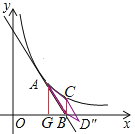
∵A（2，3）、B（4，0）、C（4，），
∴平行四边形ABD″C的面积=（梯形AGBC的面积-三角形ABG的面积）×2
=（
=3.
综上所述，平行四边形ABCD的面积为3．
故答案为：3．
