题目内容
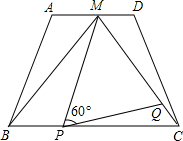 如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.(1)求证:梯形ABCD是等腰梯形;
(2)动点P、Q分别在线段BC和MC上运动,且∠MPQ=60°保持不变.设PC=x,MQ=y,求y与x的函数关系式;
(3)在(2)中:
①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当y取最小值时,判断△PQC的形状,并说明理由.
分析:(1)需证△AMB≌△DMC,可得AB=DC,可得梯形ABCD是等腰梯形;
(2)可证△BPM∽△CQP,
=
,PC=x,MQ=y,BP=4-x,QC=4-y,
=
,即可得出y=
x2-x+4;
(3)应考虑四边形ABPM和四边形MBPD均为平行四边形,四边形MPCD和四边形APCM均为平行四边形时的情况;由(2)中的函数关系,可得当y取最小值时,x=PC=2,P是BC的中点,MP⊥BC,而∠MPQ=60°,∠CPQ=30°,∠PQC=90°.
(2)可证△BPM∽△CQP,
| PC |
| BM |
| CQ |
| BP |
| x |
| 4 |
| 4-y |
| 4-x |
| 1 |
| 4 |
(3)应考虑四边形ABPM和四边形MBPD均为平行四边形,四边形MPCD和四边形APCM均为平行四边形时的情况;由(2)中的函数关系,可得当y取最小值时,x=PC=2,P是BC的中点,MP⊥BC,而∠MPQ=60°,∠CPQ=30°,∠PQC=90°.
解答:(1)证明:∵△MBC是等边三角形,
∴MB=MC,∠MBC=∠MCB=60°.(1分)
∵M是AD中点,
∴AM=MD.
∵AD∥BC,
∴∠AMB=∠MBC=60°,∠DMC=∠MCB=60°.
∴△AMB≌△DMC.(2分)
∴AB=DC.
∴梯形ABCD是等腰梯形.(3分)
(2)解:在等边△MBC中,MB=MC=BC=4,∠MBC=∠MCB=60°,∠MPQ=60°,
∴∠BMP+∠BPM=∠BPM+∠QPC=120°.
∴∠BMP=∠QPC.(4分)
∴△BPM∽△CQP.
∴
=
.(5分)
∵PC=x,MQ=y,
∴BP=4-x,QC=4-y.(6分)
∴
=
.
∴y=
x2-x+4.(7分)

(3)解:①当BP=1时,则有BP
AM,BP
MD,
则四边形ABPM为平行四边形,
∴MQ=y=
×32-3+4=
.(8分)
当BP=3时,则有PC
AM,PC
MD,
则四边形MPCD为平行四边形,
∴MQ=y=
×12-1+4=
.(9分)
∴当BP=1,MQ=
或BP=3,MQ=
时,
以P、M和A、B、C、D中的两个点为顶点的四边形是平行四边形.此时平行四边形有2个.(10分)
②△PQC为直角三角形.(11分)
∵y=
(x-2)2+3,
∴当y取最小值时,x=PC=2.(12分)
∴P是BC的中点,MP⊥BC,而∠MPQ=60°,
∴∠CPQ=30°,
∴∠PQC=90°.
∴△PQC是直角三角形.(13分)
∴MB=MC,∠MBC=∠MCB=60°.(1分)
∵M是AD中点,
∴AM=MD.
∵AD∥BC,
∴∠AMB=∠MBC=60°,∠DMC=∠MCB=60°.
∴△AMB≌△DMC.(2分)
∴AB=DC.
∴梯形ABCD是等腰梯形.(3分)
(2)解:在等边△MBC中,MB=MC=BC=4,∠MBC=∠MCB=60°,∠MPQ=60°,
∴∠BMP+∠BPM=∠BPM+∠QPC=120°.
∴∠BMP=∠QPC.(4分)
∴△BPM∽△CQP.
∴
| PC |
| BM |
| CQ |
| BP |
∵PC=x,MQ=y,
∴BP=4-x,QC=4-y.(6分)
∴
| x |
| 4 |
| 4-y |
| 4-x |
∴y=
| 1 |
| 4 |

(3)解:①当BP=1时,则有BP
| ||
. |
| ||
. |
则四边形ABPM为平行四边形,
∴MQ=y=
| 1 |
| 4 |
| 13 |
| 4 |
当BP=3时,则有PC
| ||
. |
| ||
. |
则四边形MPCD为平行四边形,
∴MQ=y=
| 1 |
| 4 |
| 13 |
| 4 |
∴当BP=1,MQ=
| 13 |
| 4 |
| 13 |
| 4 |
以P、M和A、B、C、D中的两个点为顶点的四边形是平行四边形.此时平行四边形有2个.(10分)
②△PQC为直角三角形.(11分)
∵y=
| 1 |
| 4 |
∴当y取最小值时,x=PC=2.(12分)
∴P是BC的中点,MP⊥BC,而∠MPQ=60°,
∴∠CPQ=30°,
∴∠PQC=90°.
∴△PQC是直角三角形.(13分)
点评:本题考查平行四边形、直角三角形和等腰梯形的判定以及相似三角形的判定和性质的应用.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=