Question

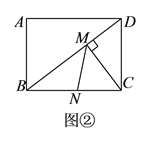
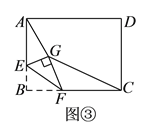
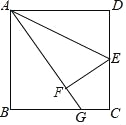
【题目】如图，在矩形ABCD中，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE，且点F在矩形ABCD的内部，将AF延长后交边BC于点G，且，则的值为__．

Answer 1

【答案】

【解析】

根据中点定义可得DE=CE，再根据翻折的性质可得DE=EF，AF=AD，∠AFE=∠D=90°，从而得到CE=EF，连接EG，利用“HL”证明Rt△ECG和Rt△EFG全等，根据全等三角形对应边相等可得CG=FG，设CG=a，表示出GB，然后求出BC，再根据矩形的对边相等可得AD=BC，从而求出AF，再求出AG，然后利用勾股定理求出AB，再求比值即可．

解：如图，连接GE．

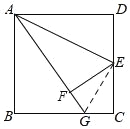
∵四边形ABCD是矩形，∴AD=BC．

∵点E是边CD的中点，∴DE=CE．

∵将△ADE沿AE折叠后得到△AFE，∴DE=EF，AF=AD，∠AFE=∠D=90°，∴CE=EF．在Rt△ECG和Rt△EFG中，，

∴Rt△ECG≌Rt△EFG（HL），

∴CG=FG．

∵=，

∴设CG=2a=FG，BC=7a，

∴BG=5a，AD=AF=7a，

∴AG=9a．

在Rt△ABG中，AB==a，

∴=．

故答案为：．