题目内容
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为 ![]() ,则AE的长为( )
,则AE的长为( ) 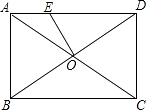
A.![]()
B.2
C.1.5
D.![]()
【答案】C
【解析】解:连接BE,如图所示: 
由题意可得,OE为对角线BD的垂直平分线,
∴BE=DE,S△BOE=S△DOE= ![]() ,
,
∴S△BDE=2S△BOE= ![]() .
.
∴ ![]() DEAB=
DEAB= ![]() ,
,
又∵AB=2,
∴DE= ![]() ,
,
∴BE= ![]()
在Rt△ABE中,由勾股定理得:AE= ![]() =
= ![]() =1.5.
=1.5.
故选:C.
首先连接BE,由题意可得OE为对角线BD的垂直平分线,可得BE=DE,S△BOE=S△DOE= ![]() ,由三角形的面积则可求得DE的长,得出BE的长,然后由勾股定理求得答案.
,由三角形的面积则可求得DE的长,得出BE的长,然后由勾股定理求得答案.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
