题目内容
已知:如下图,△ABC中,CD⊥AB于D,AC=4,BC=3,DB=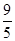 .
.
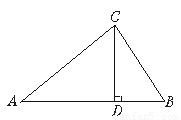
(1)求DC的长;
(2)求AD的长;
(3)求AB的长;
(4)求证:△ABC是直角三角形.
【答案】
(1)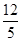 ;(2)
;(2)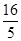 ;(3)5;(4)见解析
;(3)5;(4)见解析
【解析】
试题分析:先根据勾股定理求得DC、AD的长,即可求得AB的长,再根据勾股定理的逆定理即可证得结论.
(1)在Rt△DCB中,DC2+DB2=BC2
∴DC2=9-
∴DC=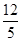 ;
;
(2)在Rt△ACD中,AD2+CD2=AC2
∴AD2=16-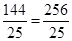
∴AD=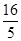 ;
;
(3)AB=AD+DB=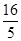 +
+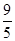 =5;
=5;
(4)∵AC2+BC2=16+9=25,AB2=25
∴AC2+BC2=AB2
∴∠ACB=90°,
∴△ABC是直角三角形.
考点:勾股定理,直角三角形的判定
点评:勾股定理是初中数学学习中一个非常重要的知识点,在很多与直角三角形相关的计算题中都有出现,因而是中考的热点,在各种题型中均有出现,需多加关注.

练习册系列答案
相关题目
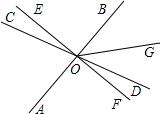 已知:如下图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.
已知:如下图,AB,CD,EF三直线相交于一点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.


