题目内容
已知a、b、c均为实数，且
，
化简：
．
解：∵
+a=0，
∴=-a．
∴a≤0，
∵
=1，
∴ab＞0，则a，b同号．
∴a＜0，b＜0．
∵
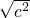=c，
∴c≥0．
∴a+b＜0，a-c＜0，c-b＞0．
∴原式=-b+（a+b）+（c-a）-（c-b）=-b+a+b+c-a-c+b=b．
分析：首先根据已知条件确定a，b，c的符号，从而确定a+b，a-c，c-b的符号，然后根据平方根，绝对值的定义即可化简求解．
点评：本题考查了二次根式的化简以及绝对值的意义，正确确定a，b，c的符号是关键．
+a=0，∴
=-a．∴a≤0，
∵
=1，∴ab＞0，则a，b同号．
∴a＜0，b＜0．
∵
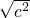=c，∴c≥0．
∴a+b＜0，a-c＜0，c-b＞0．
∴原式=-b+（a+b）+（c-a）-（c-b）=-b+a+b+c-a-c+b=b．
分析：首先根据已知条件确定a，b，c的符号，从而确定a+b，a-c，c-b的符号，然后根据平方根，绝对值的定义即可化简求解．
点评：本题考查了二次根式的化简以及绝对值的意义，正确确定a，b，c的符号是关键．
练习册系列答案
习题精选系列答案
相关题目
（2003•河南）为了了解中学生的身体素质情况，现抽取了某校实初中三年级50名学生，对每各学生进行了100米跑，立定跳远、掷铅球三个项目的测试，每个项目满分10分，图为将学生所得的三项成绩（成绩均为整数）之和进行整理后，分成五组画出频率分布直方图．已知从左到右前四个小组的频率分别是0.02，0.1，0.12，0，46，根据已知条件及图形提供的信息下列问题：
的方程
有实根.
的值;
的所有根均为整数，求整数
的值