题目内容
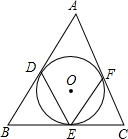
 如图,△ABC的三边分别切⊙O于D、E、F,若∠A=50°,则∠DEF=________°.
如图,△ABC的三边分别切⊙O于D、E、F,若∠A=50°,则∠DEF=________°.
65
分析:连OD,OF.则得到∠DOF与∠DEF的数量关系.而∠DOF与∠A是互补的,因此先求出∠DOF,再就能得到角DEF.
解答: 解:连OD,OF,如图,
解:连OD,OF,如图,
则OD⊥AB,OF⊥AC;
∴∠DOF=180°-∠A=180°-50°=130°,
又∵∠DEF= ∠DOF=
∠DOF= ×130°=65°,
×130°=65°,
故填65°.
点评:熟练掌握切线的性质定理和圆周角定理.记住四边形的内角和为360°.
分析:连OD,OF.则得到∠DOF与∠DEF的数量关系.而∠DOF与∠A是互补的,因此先求出∠DOF,再就能得到角DEF.
解答:
 解:连OD,OF,如图,
解:连OD,OF,如图,则OD⊥AB,OF⊥AC;
∴∠DOF=180°-∠A=180°-50°=130°,
又∵∠DEF=
 ∠DOF=
∠DOF= ×130°=65°,
×130°=65°,故填65°.
点评:熟练掌握切线的性质定理和圆周角定理.记住四边形的内角和为360°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC的三边分别切⊙O于D,E,F,若∠A=40°,则∠DEF=
如图,△ABC的三边分别切⊙O于D,E,F,若∠A=40°,则∠DEF=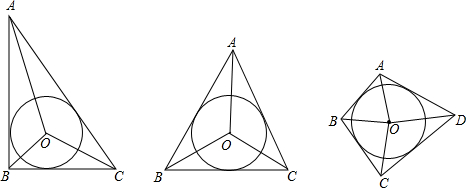
 如图,△ABC的三边AB、BC、AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC=
如图,△ABC的三边AB、BC、AC的长分别为4,6,8,其三条角平分线将△ABC分成三个三角形,则S△OAB:S△OBC:S△OAC= 如图,△ABC的三边长分别为AC=12,AB=15,BC=9.若将△ABC沿线段AD折叠,点C正好落在AB边上的点E处.求线段CD的长度.
如图,△ABC的三边长分别为AC=12,AB=15,BC=9.若将△ABC沿线段AD折叠,点C正好落在AB边上的点E处.求线段CD的长度.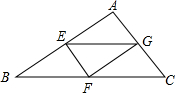 如图,△ABC的三边长分别是6cm、8cm、10cm,现在分别取三边的中点E、F、G,顺次连接E、F、G,则△EFG的面积为
如图,△ABC的三边长分别是6cm、8cm、10cm,现在分别取三边的中点E、F、G,顺次连接E、F、G,则△EFG的面积为