题目内容
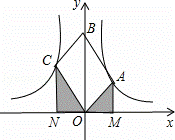
如图,OABC是平行四边形,对角线OB在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y= 和y=
和y= 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
①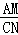 =
=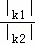 ;
;
②阴影部分面积是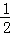 (k1+k2);
(k1+k2);
③当∠AOC=90°时,|k1|=|k2|;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确的结论是 (把所有正确的结论的序号都填上).
①④
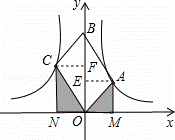
解:作AE⊥y轴于E,CF⊥y轴于F,如图,
∵四边形OABC是平行四边形,
∴S△AOB=S△COB,
∴AE=CF,
∴OM=ON,
∵S△AOM=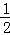 |k1|=
|k1|=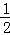 OM•AM,S△CON=
OM•AM,S△CON=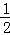 |k2|=
|k2|=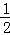 ON•CN,
ON•CN,
∴ =
=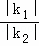 ,所以①正
,所以①正 确;
确;
∵S△AOM=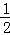 |k1|,S△CON=
|k1|,S△CON=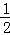 |k2|,
|k2|,
∴S阴影部分=S△AOM+S△CON=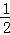 (|k1|+|k2|),
(|k1|+|k2|),
而k1>0,k2<0,
∴S阴影部分=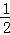 (k1﹣k2),所以②错误;
(k1﹣k2),所以②错误;
当∠AOC=90°,
∴四边形OABC是矩形,
∴不能确定OA与OC相等,
而OM=ON,
∴不能判断△AOM≌△CNO,
∴不能判断AM=CN,
∴不能确定|k1|=|k2|,所以③错误;
若OABC是菱形,则OA=OC,
而OM=ON,
∴Rt△AOM≌Rt△CNO,
∴AM=CN,
∴|k1|=|k2|,
∴k1=﹣k2,
∴两双曲线既关于x轴对称,也关于y轴对称,所以④正确.
故答案为①④.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
下列命题是假命题的是( )
|
| A. | 四个角相等的四边形是矩形 | B. | 对角线相等的平行四边形是矩形 |
|
| C. | 对角线垂直的四边形是菱形 | D. | 对角线垂直的平行四边形是菱形 |
 与l1,l2重合,AB=4
与l1,l2重合,AB=4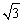 cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).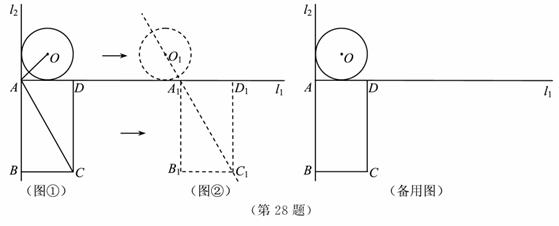

 数据:
数据: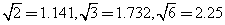 )
)