题目内容
在给出的三个多项式
x2+x-1,
x2+3x+1,
x2-x中请你选择两个进行加法运算,并把结果分解因式
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
x(x+4)或(x+1)(x-1)或(x+1)2
x(x+4)或(x+1)(x-1)或(x+1)2
.分析:选择第一个与第二个,第一个与第三个,第二个与第三个,利用整式的加法运算法则计算,然后再利用提公因式法或平方差公式或完全平方公式进行因式分解即可.
解答:解:选择第一个与第二个:(
x2+x-1)+(
x2+3x+1),
=
x2+x-1+
x2+3x+1,
=x2+4x,
=x(x+4);
第一个与第三个:(
x2+x-1)+(
x2-x),
=
x2+x-1+
x2-x,
=x2-1,
=(x+1)(x-1);
第二个与第三个:(
x2+3x+1)+(
x2-x),
=
x2+3x+1+
x2-x,
=x2+2x+1,
=(x+1)2.
故答案为:x(x+4)或(x+1)(x-1)或(x+1)2.
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=x2+4x,
=x(x+4);
第一个与第三个:(
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=x2-1,
=(x+1)(x-1);
第二个与第三个:(
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=x2+2x+1,
=(x+1)2.
故答案为:x(x+4)或(x+1)(x-1)或(x+1)2.
点评:本题考查了利用提公因式法与公式法分解因式,以及整式的加减运算,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 ,
, ,
,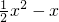 中请你选择两个进行加法运算,并把结果分解因式________.
中请你选择两个进行加法运算,并把结果分解因式________.