如图.⊙O中.ABDC是圆内接四边形.∠BOC=110°.则∠A=55°.∠BDC=125°．题目和参考答案——青夏教育精英家教网—

题目内容

14．

如图，⊙O中，ABDC是圆内接四边形，∠BOC=110°，则∠A=55°，∠BDC=125°．

分析先根据圆周角定理求出∠A的度数，再由圆内接四边形的性质求出∠BDC的度数即可．

解答解：∵∠BOC=110°，
∴∠A=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×110°=55°．
∵四边形ABDC是圆内接四边形，
∴∠BDC=180°-∠A=180°-55°=125°．
故答案为：55°，125°．

点评本题考查的是圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．

练习册系列答案

相关题目

4．

如图是由6个相同的小正方体搭成的几何体，那么这个几何体从左边看到的形状图是（　　）

5．若|a|=|b|，则a与b的关系是（　　）

2．若|a|=3，|b|=2，且|a+b|=|a|+|b|，则a+b的值是（　　）

9．10名学生参加数学竞赛，他们的成绩以80分为标准分，超过的分数记为正数，不足的分数记为负数，平分记录如下：
+10，+15，-10，-9，-8，-1，+2，-3，-2，+1．
问：（1）求这十名学生的达标率？
（2）这十名学生的成绩的平均分是否超过了标准分，平均分是多少？

19．设有x家公司参加一次商品交易会，每两家之间都签订一份合同，所有公司共签订45份合同，列方程得$\frac{1}{2}$x（x-1）=45．

6．如图所示，已知抛物线C₀的解析式为y=x²-2x
（1）求抛物线C₀的顶点坐标；
（2）将抛物线C₀每次向右平移2个单位，平移n次，依次得到抛物线
C₁，C₂，C₃…C_n（n为正整数）
①求抛物线C₂与x轴的交点A₂、A₃的坐标及它的顶点坐标；
②试确定抛物线C_n的解析式．（直接写出答案，不需要解题过程）

3．

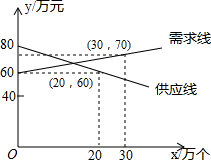某电子厂家经过市场调查发现，某种计算器的供应量x₁（万个）与价格y₁（万元）之间的关系和需求量x₂（万个）与价格y₂（万元）之间的关系如图所示，如果你是这个电子厂的厂长，你会计划生产这种计算器多少万个？每个售价多少元？才能使市场达到供需平衡？

4．若|a-1|+|b-2|=0，那么2ab=（　　）

试题分类