题目内容
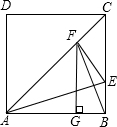 已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.下列结论①BF⊥AC,②CE2=2BE2,③AB2=2FG2.其中正确的是
已知:在正方形ABCD中,∠BAC的平分线交BC于E,作EF⊥AC于F,作FG⊥AB于G.下列结论①BF⊥AC,②CE2=2BE2,③AB2=2FG2.其中正确的是
- A.①②
- B.①③
- C.②③
- D.③
C
分析:①由于过直线上一点只有一条直线与这条直线垂直,因为EF⊥AC于F,所以BF不可能垂直于AC;
②根据四边形ABCD是正方形可得出∠ACB=90°,由勾股定理可得出CE2=2EF2,再根据角平分线的性质可得到EF=BE,进而可得出结论;
③根据AE是∠BAC的平分线可得到EF=EB,再由正方形的性质及勾股定理可得到AF2=2FG2,利用等量代换即可得出结论.
解答:①∵过直线上一点只有一条直线与这条直线垂直,
∵EF⊥AC于F,
∴BF⊥AC不成立;
②∵四边形ABCD是正方形,
∴∠ABC=90°,
∵EF⊥AC,
∴∠CFE=90°,
∴EF=CF,
∵CE2=EF2+CF2,
∴CE2=2EF2,
∵AE是∠BAC的平分线,
∴EF=BE,
∴CE2=2BE2,故此结论成立;
③∵AE是∠BAC的平分线,EF⊥AC,EB⊥AB,
∴EF=EB,
∵AE=AE,
∴△AEF≌△AEB,
∴AF=AB,
∵FG⊥AB,∠CAB=45°,
∴AG=FG,
∴AF2=2FG2,
∴AB2=2FG2,故此结论成立.
故选C.
点评:本题考查的是正方形的性质、勾股定理、角平分线的性质,涉及面较广,难度适中.
分析:①由于过直线上一点只有一条直线与这条直线垂直,因为EF⊥AC于F,所以BF不可能垂直于AC;
②根据四边形ABCD是正方形可得出∠ACB=90°,由勾股定理可得出CE2=2EF2,再根据角平分线的性质可得到EF=BE,进而可得出结论;
③根据AE是∠BAC的平分线可得到EF=EB,再由正方形的性质及勾股定理可得到AF2=2FG2,利用等量代换即可得出结论.
解答:①∵过直线上一点只有一条直线与这条直线垂直,
∵EF⊥AC于F,
∴BF⊥AC不成立;
②∵四边形ABCD是正方形,
∴∠ABC=90°,
∵EF⊥AC,
∴∠CFE=90°,
∴EF=CF,
∵CE2=EF2+CF2,
∴CE2=2EF2,
∵AE是∠BAC的平分线,
∴EF=BE,
∴CE2=2BE2,故此结论成立;
③∵AE是∠BAC的平分线,EF⊥AC,EB⊥AB,
∴EF=EB,
∵AE=AE,
∴△AEF≌△AEB,
∴AF=AB,
∵FG⊥AB,∠CAB=45°,
∴AG=FG,
∴AF2=2FG2,
∴AB2=2FG2,故此结论成立.
故选C.
点评:本题考查的是正方形的性质、勾股定理、角平分线的性质,涉及面较广,难度适中.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
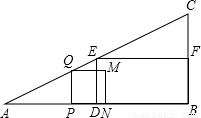
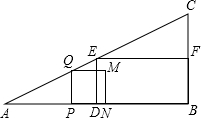 作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y. 我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.
我们定义:“四个顶点都在三角形边上的正方形是三角形的内接正方形”.