题目内容

我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形”．
已知：在Rt△ABC中，∠C=90°，AC=6，BC=3．
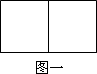
（1）如图1，四边形CDEF是△ABC的内接正方形，则正方形CDEF的边长a1是
2
2
；
（2）如图2，四边形DGHI是（1）中△EDA的内接正方形，则第2个正方形DGHI的边长a2=
4
3
4
3
；继续在图2中的△HGA中按上述方法作第3个内接正方形；…以此类推，则第n个内接正方形的边长an=
2n
3n-1
2n
3n-1
．（n为正整数）
分析：（1）由正方形的性质可以得出△BFE∽△BCA，再根据相似三角形的性质就可以把正方形CDEF的边长表示出来，从而得出结论．
（2）由正方形的性质可以得出△EIH∽△EDA，再根据相似三角形的性质就可以把正方形IDGF的边长表示出来，从而得出结论，通过计算得出的结论寻找其中的变化规律就可以得出第n个内接正方形的边长的值．
解答：解：（1）四边形CDEF是正方形，
∴EF=FC，EF∥FC，
∴△BFE∽△BCA，
∴
BF
BC
=
EF
AC
．设EF=FC=a，
∴
3-a
3
=
a
6
，
∴a=2，
故答案是：2
（2）如图（2）四边形DGHI是正方形，
∴IH=ID，IH∥AD，
∴△EIH∽△EDA，
∴
IE
DE
=
IH
AD
，设IH=ID=b，AD=4，DE=2，
∴
2-b
2
=
b
4
，
∴b=
4
3
，
故答案是：
4
3
，
如图（3）由以上同样的方法可以求得正方形PGQS的边长为：
8
9
=
23
32
，
∴第4的个正方形的边长为：
16
27
=
24
33
…
∴第n个内接正方形的边长an=
2n
3n-1

故答案为：
2n
3n-1
．
点评：本题考查了正方形的性质的运用，相似三角形的判定与性质，勾股定理的运用及规律的探索．
练习册系列答案
相关题目
定义：在平面内，我们把既有大小又有方向的量叫做平面向量．平面向量可以用有向线段表示，有向线段的长度表示向量的大小，有向线段的方向表示向量的方向．其中大小相等，方向相同的向量叫做相等向量．
如以正方形ABCD的四个顶点中某一点为起点，另一个顶点为终点作向量，可以作出8个不同的向量：
AB
、
BA
、
AC
、
CA
、
AD
、
DA
、
BD
、
DB
（由于
AB
和
DC
是相等向量，因此只算一个）．
（1）作两个相邻的正方形（如图一）．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（2），试求f（2）的值；
精英家教网
（2）作n个相邻的正方形（如图二）“一字型”排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（n），试求f（n）的值；
精英家教网
（3）作2×3个相邻的正方形（如图三）排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（2×3），试求f（2×3）的值；
精英家教网
（4）作m×n个相邻的正方形（如图四）排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（m×n），试求f（m×n）的值．
精英家教网
定义：在平面内，我们把既有大小又有方向的量叫做平面向量．平面向量可以用有向线段表示，有向线段的长度表示向量的大小，有向线段的方向表示向量的方向．其中大小相等，方向相同的向量叫做相等向量．
如以正方形ABCD的四个顶点中某一点为起点，另一个顶点为终点作向量，可以作出8个不同的向量：
AB
、
BA
、
AC
、
CA
、
AD
、
DA
、
BD
、
DB
（由于
AB
和
DC
是相等向量，因此只算一个）．
（1）作两个相邻的正方形（如图1）．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（2），试直接写出f（2）的值；
（2）作n个相邻的正方形（如图2）“一字型”排开．以其中的一个顶点为起点，另一个顶点为终点作向量，可以作出不同向量的个数记为f（n），试直接写出f（n）的值．
精英家教网
探究问题：
（1）阅读理解：
①如图（A），在已知△ABC所在平面上存在一点P，使它到三角形顶点的距离之和最小，则称点P为△ABC的费马点，此时PA+PB+PC的值为△ABC的费马距离；
②如图（B），若四边形ABCD的四个顶点在同一圆上，则有AB•CD+BC•DA=AC•BD．此为托勒密定理；
精英家教网
（2）知识迁移：
①请你利用托勒密定理，解决如下问题：
如图（C），已知点P为等边△ABC外接圆的
BC
上任意一点．求证：PB+PC=PA；
②根据（2）①的结论，我们有如下探寻△ABC（其中∠A、∠B、∠C均小于120°）的费马点和费马距离的方法：
第一步：如图（D），在△ABC的外部以BC为边长作等边△BCD及其外接圆；
第二步：在
BC
上任取一点P′，连接P′A、P′B、P′C、P′D．易知P′A+P′B+P′C=P′A+（P′B+P′C）=P′A+
 
；
第三步：请你根据（1）①中定义，在图（D）中找出△ABC的费马点P，并请指出线段
 
的长度即为△ABC的费马距离．
精英家教网
（3）知识应用：
2010年4月，我国西南地区出现了罕见的持续干旱现象，许多村庄出现了人、畜饮水困难，为解决老百姓的饮水问题，解放军某部来到云南某地打井取水．
已知三村庄A、B、C构成了如图（E）所示的△ABC（其中∠A、∠B、∠C均小于120°），现选取一点P打水井，使从水井P到三村庄A、B、C所铺设的输水管总长度最小，求输水管总长度的最小值．
精英家教网
某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨：
定义：如果一个正方形的四个顶点都在一个三角形的边上，那么我们就把这个正方形叫做三角形的内接正方形．
结论：在探讨过程中，有三位同学得出如下结果：
甲同学：在钝角、直角、不等边锐角三角形中分别存在
1
1
个、
2
2
个、
3
3
个大小不同的内接正方形．
乙同学：在直角三角形中，两个顶点都在斜边上的内接正方形的面积较大．
任务：（1）填充甲同学结论中的数据；
（2）乙同学的结果正确吗？若不正确，请举出一个反例并通过计算给予说明，若正确，请给出证明．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网