题目内容
(2012•徐汇区二模)在Rt△ABC中,∠C=90°,AC=6,sinB=
,⊙B的半径长为1,⊙B交边CB于点P,点O是边AB上的动点.
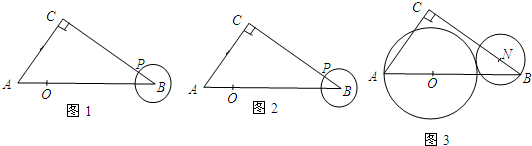
(1)如图1,将⊙B绕点P旋转180°得到⊙M,请判断⊙M与直线AB的位置关系;
(2)如图2,在(1)的条件下,当△OMP是等腰三角形时,求OA的长;
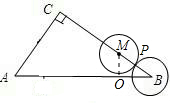
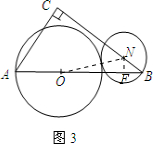
(3)如图3,点N是边BC上的动点,如果以NB为半径的⊙N和以OA为半径的⊙O外切,设NB=y,OA=x,求y关于x的函数关系式及定义域.
| 3 | 5 |
(1)如图1,将⊙B绕点P旋转180°得到⊙M,请判断⊙M与直线AB的位置关系;
(2)如图2,在(1)的条件下,当△OMP是等腰三角形时,求OA的长;
(3)如图3,点N是边BC上的动点,如果以NB为半径的⊙N和以OA为半径的⊙O外切,设NB=y,OA=x,求y关于x的函数关系式及定义域.

分析:(1)过点M作MD⊥AB,垂足为D,根据MB=2,结合sin∠B的值,可得出MD的长,与圆M的半径进行比较即可得出⊙M与直线AB的位置关系;
(2)根据(1)得出MD>MP,OM>MP,从而△OMP是等腰三角形可分两种情况讨论,①OP=MP,②OM=OP,分别运用相似三角形的性质求解OA即可;
(3)先表示出NF、BF,从而可得出OF的表达式,由⊙N和⊙O外切,可得出ON=x+y,在Rt△NFO中利用勾股定理,可得出y与x的关系式,也可得出自变量的定义域.
(2)根据(1)得出MD>MP,OM>MP,从而△OMP是等腰三角形可分两种情况讨论,①OP=MP,②OM=OP,分别运用相似三角形的性质求解OA即可;
(3)先表示出NF、BF,从而可得出OF的表达式,由⊙N和⊙O外切,可得出ON=x+y,在Rt△NFO中利用勾股定理,可得出y与x的关系式,也可得出自变量的定义域.
解答: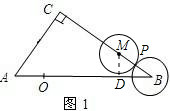 解:(1)⊙M与直线AB相离,理由如下:
解:(1)⊙M与直线AB相离,理由如下:
在Rt△ABC中,∠ACB=90°,
∵sinB=
=
,AC=6,
∴AB=10,BC=
=
=8.
过点M作MD⊥AB,垂足为D,
在Rt△MDB中,∠MDB=90°,sinB=
=
,
∵MB=2,
∴MD=
×2=
>1,
故可得⊙M与直线AB相离;
 (2)∵MD=
(2)∵MD=
>1=MP,
∴OM>MP.
分两种情况讨论,
1°当OP=MP时,此时OP=MP=PB,
故易得∠MOB=90°,
∴cosB=
=
=
,
∴OB=
,
∴OA=
;
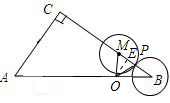
2°当OM=OP时,过点O作OE⊥BC,垂足为E
EB=EP+PB=
+1=
,
 此时cosB=
此时cosB=
=
=
,
∴OB=
,
∴OA=
.
综上可得,当△OMP是等腰三角形时,OA的长为
或
;
(3)连接ON,过点N作NF⊥AB,垂足为F.
 在Rt△NFB中,∠NFB=90°,sinB=
在Rt△NFB中,∠NFB=90°,sinB=
,
设NB=y,则NF=
y,BF=
y,
故可得OF=10-x-
y,
∵⊙N和⊙O外切,
∴ON=x+y,
在Rt△NFO中,∠NFO=90°,则ON2=OF2+NF2,
即(x+y)2=(10-x-
y)2+(
y)2,
故可得y=
,定义域为:0<x<5.
 解:(1)⊙M与直线AB相离,理由如下:
解:(1)⊙M与直线AB相离,理由如下:在Rt△ABC中,∠ACB=90°,
∵sinB=
| AC |
| AB |
| 3 |
| 5 |
∴AB=10,BC=
| AB2-AC2 |
| 102-62 |
过点M作MD⊥AB,垂足为D,
在Rt△MDB中,∠MDB=90°,sinB=
| MD |
| MB |
| 3 |
| 5 |
∵MB=2,
∴MD=
| 3 |
| 5 |
| 6 |
| 5 |
故可得⊙M与直线AB相离;
 (2)∵MD=
(2)∵MD=| 6 |
| 5 |
∴OM>MP.
分两种情况讨论,
1°当OP=MP时,此时OP=MP=PB,
故易得∠MOB=90°,
∴cosB=
| OB |
| BM |
| BC |
| AB |
| 8 |
| 10 |
∴OB=
| 8 |
| 5 |
∴OA=
| 42 |
| 5 |
2°当OM=OP时,过点O作OE⊥BC,垂足为E
EB=EP+PB=
| 1 |
| 2 |
| 3 |
| 2 |
 此时cosB=
此时cosB=| EB |
| OB |
| BC |
| AB |
| 8 |
| 10 |
∴OB=
| 15 |
| 8 |
∴OA=
| 65 |
| 8 |
综上可得,当△OMP是等腰三角形时,OA的长为
| 42 |
| 5 |
| 65 |
| 8 |
(3)连接ON,过点N作NF⊥AB,垂足为F.
 在Rt△NFB中,∠NFB=90°,sinB=
在Rt△NFB中,∠NFB=90°,sinB=| 3 |
| 5 |
设NB=y,则NF=
| 3 |
| 5 |
| 4 |
| 5 |
故可得OF=10-x-
| 4 |
| 5 |
∵⊙N和⊙O外切,
∴ON=x+y,
在Rt△NFO中,∠NFO=90°,则ON2=OF2+NF2,
即(x+y)2=(10-x-
| 4 |
| 5 |
| 3 |
| 5 |
故可得y=
| 250-50x |
| x+40 |
点评:此题属于圆的综合题,涉及了直线与圆的位置关系、勾股定理及等腰三角形的性质,综合性较强,难点在第二问和第三问,解答时注意分类讨论思想的运用,另外要求我们能将所学知识融会贯通.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 (2012•徐汇区二模)如图,矩形ABCD中,AB=2,BC=4,点A、B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是
(2012•徐汇区二模)如图,矩形ABCD中,AB=2,BC=4,点A、B分别在y轴、x轴的正半轴上,点C在第一象限,如果∠OAB=30°,那么点C的坐标是