题目内容
8.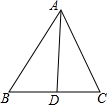 如图,△ABC中,∠BAC的平分线为AD,∠ADC=80°,∠BAC比∠B大10°,求△ABC的三个内角的度数.
如图,△ABC中,∠BAC的平分线为AD,∠ADC=80°,∠BAC比∠B大10°,求△ABC的三个内角的度数.
分析 根据已知条件得到∠BAD=$\frac{1}{2}$(∠B+10°),由三角形的外角的性质列方程∠ADC=∠B+∠BAD=∠B+$\frac{1}{2}$(∠B+10°)=80°,求得∠B=50°,得到∠BAC=60°,根据三角形的内角和得到∠C=180°-∠B-∠BAC=70°.
解答 解:∵∠BAC比∠B大10°,
∴∠BAC=∠B+10°,
∵∠BAC的平分线为AD,
∴∠BAD=$\frac{1}{2}$(∠B+10°),
∵∠ADC=∠B+∠BAD=∠B+$\frac{1}{2}$(∠B+10°)=80°,
∴∠B=50°,
∴∠BAC=60°,
∴∠C=180°-∠B-∠BAC=70°.
∴△ABC的三个内角的度数分别为:50°60°,70°.
点评 本题考查了三角形的内角和,三角形的外角的性质,角平分线的定义,熟记三角形的内角和是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.某区从参加地理学业水平考试的8000名学生中,随机抽取了部分学生的成绩作为样本,为了节省时间,先将样本分成甲、乙两组,分别进行分析,得到下表;随后汇总整个样本数据,得到部分结果,绘制成如下统计图.
(注:A:优秀(≥90分)、B:良好(≥70分且<90分)、C:及格(≥60分且<70分)、D:不及格(<60分))
表一
请根据图和表所示信息回答下列问题:
(1)样本中,学生地理学成绩平均分为B分,中位数在B内(填等第),众数是
B(填等第).A占的百分比是30%,C占的百分比是15%.
(2)补全条形统计图.
(3)成绩不低于60的为合格,估计这8000名学生的合格人数.

(注:A:优秀(≥90分)、B:良好(≥70分且<90分)、C:及格(≥60分且<70分)、D:不及格(<60分))
表一
| 甲组 | 乙组 | |
| 人数(人) | 120 | 80 |
| 平均分(分) | 88 | 83 |
(1)样本中,学生地理学成绩平均分为B分,中位数在B内(填等第),众数是
B(填等第).A占的百分比是30%,C占的百分比是15%.
(2)补全条形统计图.
(3)成绩不低于60的为合格,估计这8000名学生的合格人数.

17.已知不等式组$\left\{\begin{array}{l}{x+2>1}\\{x+3≤5}\end{array}\right.$,则该不等式组的解集(阴影部分)在数轴上表示正确的是( )
| A. | 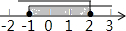 | B. |  | C. | 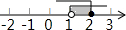 | D. | 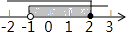 |
18.某校九(1)班同学积极参加社团活动,每人均参加篮球、书法、舞蹈和象棋其中的一项,小明同学调查后,整理相关数据并制作了两个不完整的统计图:
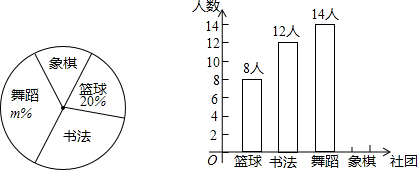
根据以上信息解答下列问题:
(1)请补全条形统计图,并直接写出扇形统计图中的m=35
(2)学校对该班社团活动进行测评,各社团的平均得分如表:
求九(1)班社团测评的平均分.

根据以上信息解答下列问题:
(1)请补全条形统计图,并直接写出扇形统计图中的m=35
(2)学校对该班社团活动进行测评,各社团的平均得分如表:
| 社团 | 篮球 | 书法 | 舞动 | 象棋 |
| 平均分 | 4 | 4.5 | 3 | 4 |
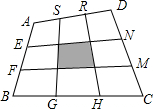 如图,已知四边形ABCD中E,F,G,H,N、N,R、S分别是四边形三等分点,求证:S阴影=$\frac{1}{9}$S四边形ABCD.
如图,已知四边形ABCD中E,F,G,H,N、N,R、S分别是四边形三等分点,求证:S阴影=$\frac{1}{9}$S四边形ABCD. 如图,某拦河坝横截面原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°,为了提高拦河坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°,请你计算这个拦河大坝的高度.(参考数据:sin72°≈$\frac{12}{13}$,cos72°≈$\frac{5}{13}$,tan72°$≈\frac{12}{5}$)
如图,某拦河坝横截面原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°,为了提高拦河坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°,请你计算这个拦河大坝的高度.(参考数据:sin72°≈$\frac{12}{13}$,cos72°≈$\frac{5}{13}$,tan72°$≈\frac{12}{5}$)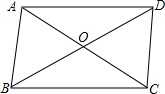 如图,在?ABCD中,对角线AC、BD相交成的锐角为60°,若AC=6,BD=8,求?ABCD的面积.($\sqrt{3}≈1.73$,结果精确到0.1)
如图,在?ABCD中,对角线AC、BD相交成的锐角为60°,若AC=6,BD=8,求?ABCD的面积.($\sqrt{3}≈1.73$,结果精确到0.1)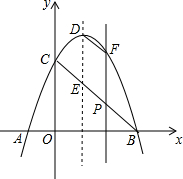 如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=-x2+bx+c与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,线段BC与抛物线的对称轴交于点E、P为线段BC上的一点(不与点B、C重合),过点P作PF∥y轴交抛物线于点F,连结DF.设点P的横坐标为m.