题目内容
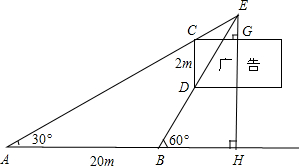 如图,竖直立着的水泥柱子上挂着一个矩形广告牌,已知CD=2m,且CD与水平地面AH垂直,经过测量得到的数据如图所示.其中∠CAH=30°,∠DBH=60°,AB=20m,点A、B、H在一条直线上.视线AC和BD交于点E,请根据以上数据计算广告牌的高度GH.(
如图,竖直立着的水泥柱子上挂着一个矩形广告牌,已知CD=2m,且CD与水平地面AH垂直,经过测量得到的数据如图所示.其中∠CAH=30°,∠DBH=60°,AB=20m,点A、B、H在一条直线上.视线AC和BD交于点E,请根据以上数据计算广告牌的高度GH.(| 3 |
考点:解直角三角形的应用-仰角俯角问题
专题:
分析:设DE=x,则CE=x+2,通过解直角三角形得到:AE=
(x+2),BE=
x,进而求出x的长,进而得出GH的长.
| 3 |
| ||
| 3 |
解答: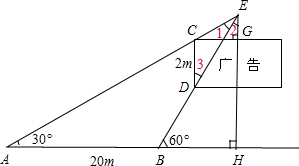 解:依题意得:
解:依题意得:
∠1=60°-30°=30°.
在Rt△BEH中,∠2=90°-60°=30°,∠1=∠2.
∵EH∥CD,
∴∠2=∠3,
∴∠1=∠3.
∴CE=CD=2cm.
在Rt△EOG中,∠CEG=60°,EG=
CG=1.
∵∠1=∠A=30°,
∴AE=EB=20.
在Rt△EBH中,EH=EB•sin60°=20×
=10
∴GH=EH-EG=10
-1≈10×1.732-1≈16.3.
答:广告牌的高度GH是16.3m.
 解:依题意得:
解:依题意得:∠1=60°-30°=30°.
在Rt△BEH中,∠2=90°-60°=30°,∠1=∠2.
∵EH∥CD,
∴∠2=∠3,
∴∠1=∠3.
∴CE=CD=2cm.
在Rt△EOG中,∠CEG=60°,EG=
| 1 |
| 2 |
∵∠1=∠A=30°,
∴AE=EB=20.
在Rt△EBH中,EH=EB•sin60°=20×
| ||
| 2 |
| 3 |
∴GH=EH-EG=10
| 3 |
答:广告牌的高度GH是16.3m.
点评:此题主要考查了解直角三角形的应用--仰角俯角问题.熟记锐角三角函数定义是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
在△ABC中,AB=3,AC=
,BC=
,则tanA=( )
| 7 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知点A(2,y1)和点B(m,y2)是抛物线y=x2-2x上两点,且y2>y1,则m的取值范围是( )
| A、m>2 |
| B、m≤0或m≥2 |
| C、0<m<2 |
| D、m<0或m>2 |
把不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
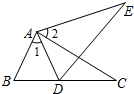 如图,在△ABC和△ADE中,B、D、C三点在同一直线上.有以下四个条件:
如图,在△ABC和△ADE中,B、D、C三点在同一直线上.有以下四个条件: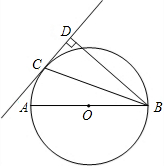 如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.
如图,点C是以AB为直径的⊙O上的一点,BD与过点C的切线互相垂直,垂足为点D.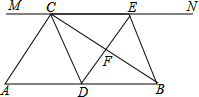 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.