题目内容
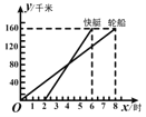
【题目】如图所示，表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程y(千米)随时间t（时）变化的图象，根据图象回答下列问题
（1）轮船的行驶速度是___________km/h;
（2）当2≤t≤6时，求快艇行驶过程y与t的函数关系式；
（3）当快艇与乙港相距40 km时，快艇和轮船相距___________km
【答案】（1）20；（2）
；（3）20；
【解析】
(1)根据速度=路程÷时间即可求得轮船行驶的速度；
(2) 设表示快艇行驶过程的函数式为y=kt+b，根据图象找出点的坐标利用待定系数法即可求出函数解析式；
(3)根据快艇与乙港相距40 km算出轮船行驶的时间，再根据（1）轮船的速度计算出此时轮船行驶的路程，再做减法即可得到答案；
解：（1）从图象可以得到，轮船行驶160千米所需的时间为8小时，
所以轮船的速度为：
km/h；
故答案为：
km/h；
(2) 设表示快艇行驶过程的函数式为y=at+b，
根据图象可知，当
时，
，当
时，
，
，解得：
，
故快艇行驶过程y与t的函数关系式为：；
(3)由（2）得到快艇行驶过程y与t的函数关系式为：，
当快艇与乙港相距40 km时，快艇行驶了
㎞，
此时得到：
，
解得
，
由（1）知轮船的行驶速度是20km/h;
根据题意得到：当，轮船行驶了
，
故快艇和轮船相距
；
练习册系列答案
相关题目
