题目内容

11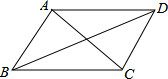．如图，在下列四组条件中，不能判断AD∥BC的是（　　）
A．∠DAC=ACBB．∠ADB=∠DBCC．∠DAB+∠ABC=180°D．∠BAC=∠ACD

分析 根据各选项中各角的关系及利用平行线的判定定理，分别分析判断AD、BC是否平行即可．

解答 解：A、∵∠DAC=∠BCA，∴AD∥BC（内错角相等，两直线平行），故A能判断；
B、∵∠ADB=∠DBC，∴AD∥BC（内错角相等，两直线平行），故B能判断；
C、根据∠DAB+∠ABC=180°，能判定AD∥BC，故C能判断；
D、根据“∠BAC=∠ACD”只能判定“DC∥AB”，而非AD∥BC，故D不能判断；
故选：D．

点评 本题主要考查了平行线的判定．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．

练习册系列答案
相关题目
1．下列各式中计算正确的是（　　）
A．$\sqrt{9}$+$\sqrt{16}$=$\sqrt{9+16}$=5B．$\sqrt{9}$=±3C．-$\sqrt{{{（{-9}）}^2}}$=9D．$\sqrt{5}$×$\sqrt{3}$=$\sqrt{15}$
2．在下列实数中$\sqrt{5}$、$\frac{22}{7}$、0、$\frac{π}{2}$、$\sqrt{36}$、$\root{3}{9}$、-1.414、$\frac{{\sqrt{2}}}{2}$是分数的有（　　）
A．6个B．4个C．2个D．以上均不对
19．下列运算正确的是（　　）
A．a6÷a2=a3B．a6+a2=a8C．（a2）3=a6D．2a×3a=6a
6．已知抛物线y=ax2+bx+c的对称轴为x=2，且经过点（-4，0），（2，6），则这个二次函数的解析式为y=-$\frac{1}{6}$x2+$\frac{2}{3}$x+$\frac{16}{3}$．
16．化简下列各数：
-（-82）=82；-（+3.73）=-3.73；-（$\frac{2}{7}$）=-$\frac{2}{7}$；|-3.7|=3.7；|0|=0；-|-3.3|=-3.3；-|+0.75|=-0.75；
|+$\frac{1}{3}$|=$\frac{1}{3}$；+|-$\frac{2}{3}$|=$\frac{2}{3}$；|-10|+|-5|=15；|-6|÷|-3|=2；|-6.5|-|-5.5|=1．
3．点（-2，4）在反比例函数y=$\frac{k}{x}$（k≠0）的图象上，则下列各点在此函数图象上的是（　　）
A．（2，4）B．（-1，-8）C．（-2，-4）D．（4，-2）
20．计算：3a•2b=6ab；  （-$\frac{1}{2}$）2013×（2）2014=-2．
1．与$\sqrt{17}$最接近的整数是（　　）
A．3B．4C．5D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网