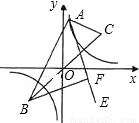
题目内容
如图,点A是函数 的图象上的点,点B、C的坐标分别为B(-
的图象上的点,点B、C的坐标分别为B(- ,-
,- )、C(
)、C( ,
, ).试利用性质:点“函数
).试利用性质:点“函数 的图象上任意一点A都满足
的图象上任意一点A都满足 ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.已知当A在函数
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.已知当A在函数 的图象上运动时,OF的长度总等于 .
的图象上运动时,OF的长度总等于 .
【答案】分析:延长BF、AC交于点G.根据全等三角形的判定,得到△ABF≌△AGF,则AB=AG,BF=GF.根据点B和点C的坐标,知点B和点C关于原点对称,则OB=OC,从而根据三角形的中位线定理,得OF= CG=
CG=
 ×
× .
.
解答: 解:延长BF、AC交于点G.
解:延长BF、AC交于点G.
∵AE是∠BAC的内角平分线,
∴∠BAF=∠GAF,
∵BF⊥AE,
∴∠AFB=∠AFG=90°,
又∵AF=AF,
∴△ABF≌△AGF,
∴AB=AG,BF=GF.
∵B(- ,-
,- )、C(
)、C( ,
, ),
),
∴OB=OC,
∴OF= CG=
CG=
 ×
× =
= .
.
故答案为: .
.
点评:此题是一道数形结合题,综合考查了全等三角形的判定和性质、三角形的中位线定理、中心对称的性质.
 CG=
CG=
 ×
× .
.解答:
 解:延长BF、AC交于点G.
解:延长BF、AC交于点G.∵AE是∠BAC的内角平分线,
∴∠BAF=∠GAF,
∵BF⊥AE,
∴∠AFB=∠AFG=90°,
又∵AF=AF,
∴△ABF≌△AGF,
∴AB=AG,BF=GF.
∵B(-
 ,-
,- )、C(
)、C( ,
, ),
),∴OB=OC,
∴OF=
 CG=
CG=
 ×
× =
= .
.故答案为:
 .
.点评:此题是一道数形结合题,综合考查了全等三角形的判定和性质、三角形的中位线定理、中心对称的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,P是反比例函数图象上的一点,且点P到x轴的距离为3,到y轴的距离为2,
如图,P是反比例函数图象上的一点,且点P到x轴的距离为3,到y轴的距离为2, 的图象上的点,点B,C的坐标分别为B(-
的图象上的点,点B,C的坐标分别为B(- ,-
,- ),C(
),C( ,
, ).试利用性质:“函数y=
).试利用性质:“函数y= 的图象上任意一点A都满足|AB-AC|=2
的图象上任意一点A都满足|AB-AC|=2 ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y= 的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )
的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )
 的图象上的点,点B,C的坐标分别为B(-
的图象上的点,点B,C的坐标分别为B(- ,-
,- ),C(
),C( ,
, ).试利用性质:“函数y=
).试利用性质:“函数y= 的图象上任意一点A都满足|AB-AC|=2
的图象上任意一点A都满足|AB-AC|=2 ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y= 的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )
的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )
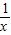 的图象上的点,点B,C的坐标分别为B(-
的图象上的点,点B,C的坐标分别为B(-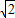 ,-
,-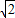 ),C(
),C(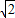 ,
, ).试利用性质:“函数y=
).试利用性质:“函数y=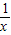 的图象上任意一点A都满足|AB-AC|=2
的图象上任意一点A都满足|AB-AC|=2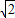 ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y=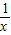 的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )
的图象上运动时,点F总在一条曲线上运动,则这条曲线为( )