题目内容
13．利用加减消元法解方程组$\left\{\begin{array}{l}{2x+5y=-10①}\\{5x-3y=6②}\end{array}\right.$，下列做法正确的是（ ）| A． | 要消去y，可以将①×5+②×2 | B． | 要消去x，可以将①×3+②×（-5） | ||
| C． | 要消去y，可以将①×5+②×3 | D． | 要消去x，可以将①×（-5）+②×2 |
分析 方程组利用加减消元法求出解即可．
解答 解：利用加减消元法解方程组$\left\{\begin{array}{l}{2x+5y=-10①}\\{5x-3y=6②}\end{array}\right.$，要消去x，可以将①×（-5）+②×2．
故选D
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
相关题目
3．
如图，AB∥CD，点E在线段BC上，若∠1=40°，∠2=30°，则∠3的度数是（ ）
如图，AB∥CD，点E在线段BC上，若∠1=40°，∠2=30°，则∠3的度数是（ ）| A． | 70° | B． | 60° | C． | 55° | D． | 50° |
4．
如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（ ）
如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（ ）| A． | ∠A=∠D | B． | AB=DC | C． | ∠ACB=∠DBC | D． | AC=BD |
18．
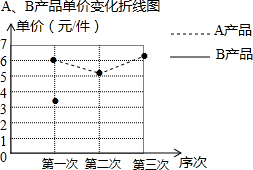某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如表统计表及不完整的折线图．
A，B产品单价变化统计表
并求得了A产品三次单价的平均数和方差：
$\overline{{x}_{A}}$=5.9，sA2=$\frac{1}{3}$[（6-5.9）2+（5.2-5.9）2+（6.5-5.9）2]=$\frac{43}{150}$
（1）补全如图中B产品单价变化的折线图．B产品第三次的单价比上一次的单价降低了25%
（2）求B产品三次单价的方差，并比较哪种产品的单价波动小；
（3）该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，求m的值．
某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如表统计表及不完整的折线图．A，B产品单价变化统计表
| 第一次 | 第二次 | 第三次 | |
| A产品单价（元/件） | 6 | 5.2 | 6.5 |
| B产品单价（元/件） | 3.5 | 4 | 3 |
$\overline{{x}_{A}}$=5.9，sA2=$\frac{1}{3}$[（6-5.9）2+（5.2-5.9）2+（6.5-5.9）2]=$\frac{43}{150}$
（1）补全如图中B产品单价变化的折线图．B产品第三次的单价比上一次的单价降低了25%
（2）求B产品三次单价的方差，并比较哪种产品的单价波动小；
（3）该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1，求m的值．
5．
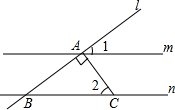如图，m∥n，直线l分别交m，n于点A，点B，AC⊥AB，AC交直线n于点C，若∠1=35°，则∠2等于（ ）
如图，m∥n，直线l分别交m，n于点A，点B，AC⊥AB，AC交直线n于点C，若∠1=35°，则∠2等于（ ）| A． | 35° | B． | 45° | C． | 55° | D． | 65° |
8．下列各数中，最小的数是（ ）
| A． | -0.5 | B． | 0 | C． | -2 | D． | 1 |