题目内容
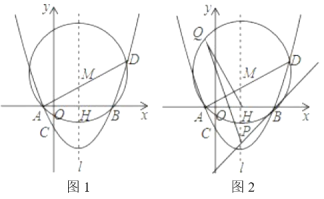
【题目】如图，在平面直角坐标系中，∠AOB=90°，AB∥x轴，OA=2，双曲线
经过点A．将△AOB绕点A顺时针旋转，使点O的对应点D落在x轴的负半轴上，若AB的对应线段AC恰好经过点O．
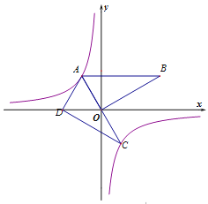
（1）求点A的坐标和双曲线的解析式；
（2）判断点C是否在双曲线上，并说明理由
【答案】（1）
，双曲线的解析式为
；（2）点
在双曲线上，理由见解析.
【解析】
（1）根据旋转的性质和平行线的性质，得到
，得到△AOD是等边三角形，根据特殊角的三角函数，求出点A的坐标，然后得到双曲线的解析式；
（2）先求出OC的长度，然后利用特殊角的三角函数求出点C的坐标，然后进行判断即可.
解：（1）过点A作
轴，垂足为
．
∵
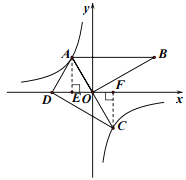
轴，
．
有旋转的性质可知
，
．
．
．
为等边三角形．
．
，
．
点
的坐标为
．
由题意知，
，
．
双曲线的解析式为：．
（2）点在双曲线上，理由如下：
过点作
轴，垂足为
．
由（1）知
，
．
．
．
，
．
点的坐标为
．
将
代入中，
．
点
在双曲线上．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
