题目内容
 “小发明家”小颖发明了一个智能电动跳跳蛙,启动后第一次从原地向前跳1cm并顺时针转90°,接着第二次向前跳2cm并顺时针转90°,再接着第三次向前跳3cm并顺时针转90°…,按此程序一直能跳下去.若将这只跳跳蛙放在一个半径为5cm的圆的圆心上,启动后,第________次跳跃后,跳跳蛙已不在圆内.
“小发明家”小颖发明了一个智能电动跳跳蛙,启动后第一次从原地向前跳1cm并顺时针转90°,接着第二次向前跳2cm并顺时针转90°,再接着第三次向前跳3cm并顺时针转90°…,按此程序一直能跳下去.若将这只跳跳蛙放在一个半径为5cm的圆的圆心上,启动后,第________次跳跃后,跳跳蛙已不在圆内.
6
分析:根据勾股定理依次求出从原地向前跳一定的长度并顺时针转90°与圆心的距离,再与半径5cm比较即可求解.
解答: 解:第一次与圆心的距离为1cm;
解:第一次与圆心的距离为1cm;
第二次与圆心的距离为 =
= cm;
cm;
第三次与圆心的距离为 =2
=2 cm;
cm;
第四次与圆心的距离为 =2
=2 cm;
cm;
第五次与圆心的距离为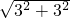 =3
=3 cm;
cm;
第六次与圆心的距离为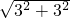 =3
=3 cm;
cm;
第七次与圆心的距离为 =5cm.
=5cm.
故第6次跳跃后,跳跳蛙已不在圆内.
故答案为:6.
点评:考查了旋转的性质,勾股定理和点与圆的位置关系,得到向前跳后各点与圆心的距离是解题的关键.
分析:根据勾股定理依次求出从原地向前跳一定的长度并顺时针转90°与圆心的距离,再与半径5cm比较即可求解.
解答:
 解:第一次与圆心的距离为1cm;
解:第一次与圆心的距离为1cm;第二次与圆心的距离为
 =
= cm;
cm;第三次与圆心的距离为
 =2
=2 cm;
cm;第四次与圆心的距离为
 =2
=2 cm;
cm;第五次与圆心的距离为
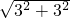 =3
=3 cm;
cm;第六次与圆心的距离为
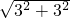 =3
=3 cm;
cm;第七次与圆心的距离为
 =5cm.
=5cm.故第6次跳跃后,跳跳蛙已不在圆内.
故答案为:6.
点评:考查了旋转的性质,勾股定理和点与圆的位置关系,得到向前跳后各点与圆心的距离是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 “小发明家”小颖发明了一个智能电动跳跳蛙,启动后第一次从原地向前跳1cm并顺时针转90°,接着第二次向前跳2cm并顺时针转90°,再接着第三次向前跳3cm并顺时针转90°…,按此程序一直能跳下去.若将这只跳跳蛙放在一个半径为5cm的圆的圆心上,启动后,第
“小发明家”小颖发明了一个智能电动跳跳蛙,启动后第一次从原地向前跳1cm并顺时针转90°,接着第二次向前跳2cm并顺时针转90°,再接着第三次向前跳3cm并顺时针转90°…,按此程序一直能跳下去.若将这只跳跳蛙放在一个半径为5cm的圆的圆心上,启动后,第
