题目内容
 如图,△ABC中,AB=AC=15,∠B=30°,在AB、AC、BC上分别取一点D、E、F,使AD=AE,BD=DF,要使△DEF和△CEF均是直角三角形,那么AD=
如图,△ABC中,AB=AC=15,∠B=30°,在AB、AC、BC上分别取一点D、E、F,使AD=AE,BD=DF,要使△DEF和△CEF均是直角三角形,那么AD=考点:勾股定理,等腰三角形的性质,含30度角的直角三角形
专题:分类讨论
分析:由于在△ABC中,AB=AC,AD=AE,可得DE∥BC,根据等腰三角形的性质和平行线的性质可得∠EDF=30°,再根据含30度角的直角三角形的性质以及勾股定理,分∠DEF=90°和∠DFE=90°两种情况讨论可求AD的长.
解答:解:∵在△ABC中,AB=AC,AD=AE,
∴DE∥BC,
∵∠B=30°,
∴∠EDF=30°,
∴当∠DEF=90°时,设AD=x,则BD=DF=15-x,DE=
x,则15-x=
×
x,解得x=6
当∠DFE=90°时,设AD=x,则BD=DF=15-x,DE=
x,则
×(15-x)=
x,解得x=5.
综上所述,AD=5或6.
故答案为:5或6.
∴DE∥BC,
∵∠B=30°,
∴∠EDF=30°,
∴当∠DEF=90°时,设AD=x,则BD=DF=15-x,DE=
| 3 |
| ||
| 2 |
| 3 |
当∠DFE=90°时,设AD=x,则BD=DF=15-x,DE=
| 3 |
| ||
| 2 |
| 3 |
综上所述,AD=5或6.
故答案为:5或6.
点评:考查了勾股定理,等腰三角形的性质和平行线的判定和性质,含30度角的直角三角形的性质,以及分类思想的运用,综合性较强,有一定的难度.

练习册系列答案
相关题目
 如图为一位旅行者从早晨8时出发到郊外所走的路程s(单位:千米)随时间t(单位:时)变化的情况,根据图象回答问题:
如图为一位旅行者从早晨8时出发到郊外所走的路程s(单位:千米)随时间t(单位:时)变化的情况,根据图象回答问题: 如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论:
如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论: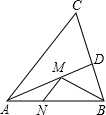 选做题:如图,在锐角△ABC中,AB=2,∠BAC=60°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是
选做题:如图,在锐角△ABC中,AB=2,∠BAC=60°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是