题目内容
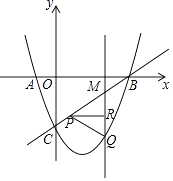
【题目】如图,抛物线y=ax2﹣(a+1)x﹣3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
(1)求抛物线的表达式;
(2)当m=2时,△PQR为等腰直角三角形,求点P的坐标;
(3)①求PR+QR的最大值;②求△PQR面积的最大值.
【答案】
(1)
解:在y=ax2﹣(a+1)x﹣3中,令x=0可得y=﹣3,
∴C(0,﹣3),即OC=3,
∵∠BCO=45°,
∴OB=OC=3,
∴B(3,0),
把B点坐标代入抛物线解析式可得9a﹣3(a+1)﹣3=0,求得a=1,
∴抛物线的表达式为y=x2﹣2x﹣3
(2)
解:当m=2时,则M(2,0),
把x=2代入抛物线解析式可得y=﹣3,
∴Q(2,﹣3),
∵B(3,0),C(0,﹣3),
∴直线BC表达式为y=x﹣3,
∴可设P(p,p﹣3),则PR=2﹣p,QR=p﹣3﹣(﹣3)=p,
∵PR=QR,
∴2﹣p=p,解得p=1,
∴P(1,﹣2)
(3)
解:①由(2)可知M(m,m﹣3),Q(m,m2﹣2m﹣3),
∵PR⊥MQ,
∴∠MPR=45°,
∴MR=PR,
∴PR+QR=PR+MR=QM=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m=﹣(m﹣ ![]() )2+
)2+ ![]() ,
,
∵﹣1<0,
∴当m= ![]() 时,PR+QR取最大值
时,PR+QR取最大值 ![]() ;
;
②∵PR+QR的最大值为 ![]() ,
,
∴S△PQR= ![]() PRQR≤
PRQR≤ ![]() PR(
PR( ![]() ﹣PR)=﹣
﹣PR)=﹣ ![]() (PR﹣
(PR﹣ ![]() )2+
)2+ ![]() ,
,
∵ ![]() <0,
<0,
∴当PR= ![]() 时,△PQR的面积取得最大值
时,△PQR的面积取得最大值 ![]() .
.
【解析】(1)可先求得C点坐标,利用∠BCO=45°可求得B点坐标,代入抛物线解析式可求得a,可求得抛物线解析式;(2)可先求得Q的坐标,利用待定系数法可求得直线BC解析式,设出P点坐标,则可表示出PR、QR的长,由等腰三角形的性质可得到关于P点坐标的方程,可求得P点坐标;(3)①由题意可知PR=RM,故PR+QR=MQ,设出可用m表示出Q点坐标,则可表示出MQ的长,利用二次函数的性质可求得其最大值;②用PR表示出△PQR的面积,利用二次函数的性质可求得其最大值.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案