Question

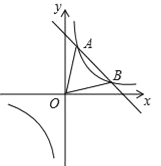
【题目】如图①，在△ABC中，AB=AC，点P为边BC上异于B和C的任意一点，过点P作PD⊥AB于D，作PE⊥AC于E，过点C作CF⊥AB于F，求证：PD+PE=CF．

（1）有下面两种证明思路：（一）如图②，连接AP，由△ABP于△ACP面积之和等于△ABC的面积证得PD+PE=CF．（二）如图②，过点P作PG⊥CF，垂足为G，可以证明：PD=GF，PE=CG，则PD+PE=CF．

请你选择其中的一种证明思路完成证明：

（2）探究：如图③，当点P在BC的延长线上时，其它条件不变，探究并证明PD、PE和CF间的数量关系；

（3）猜想：当点P在CB的延长线上时，其它条件不变，猜想PD、PE和CF间的数量关系（不要求证明）

Answer 1

【答案】（1）PD+PE=CF（2）PD﹣PE=CF（3）PE﹣PD=CF

【解析】

（1）连接AP，根据S△ABP+S△ACP=S△ABC列式整理即可得解；

（2）连接AP，根据S△ABP﹣S△ACP=S△ABC列式整理即可得解；

（3）连接AP，根据S△ACP﹣S△ABP=S△ABC列式整理即可得解.

（1）如图②，连接AP，

∵PD⊥AB，PE⊥AC，CF⊥AB，

∴S△ABP=ABPD，S△ACP=ACPE，S△ABC=ABCF，

∵S△ABP+S△ACP=S△ABC，

∴ABPD+ACPE=ABCF，

又AB=AC，

∴PD+PE=CF；

（2）PD﹣PE=CF

如图③，连接AP，

∵PD⊥AB，PE⊥AC，CF⊥AB，

∴S△ABP=ABPD，S△ACP=ACPE，S△ABC=ABCF，

∵S△ABP﹣S△ACP=S△ABC，

∴ABPD﹣ACPE=ABCF，

又∵AB=AC，

∴PD﹣PE=CF；

（3）PD﹣PE=CF，

如图4，连接AP，

∵PD⊥AB，PE⊥AC，CF⊥AB，

∴S△ABP=ABPD，S△ACP=ACPE，S△ABC=ABCF，

∵S△ACP﹣S△ABP=S△ABC，

∴ACPE﹣ABPD=ABCF，

又∵AB=AC，

∴PE﹣PD=CF；