Question

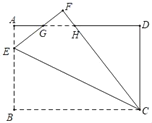
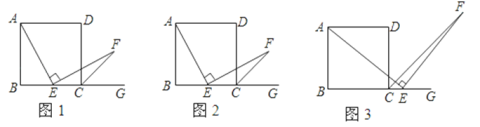
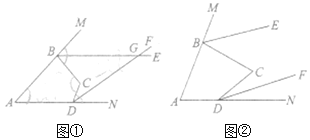
【题目】如图①，、分别平分四边形的外角和，设，．

（1）若，则 ；

（2）若与相交于点，且，求、所满足的等量关系式，并说明理由；

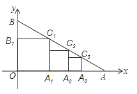
（3）如图②，若，试判断、的位置关系，并说明理由．

Answer 1

【答案】（1）110；（2），理由见解析；（3），理由见解析

【解析】

（1）根据四边形的内角和与邻补角的性质即可求解；

（2）连接BD，先得到，再根据三角形的内角和得到角度的关系即可求解；

（3）由（1）有，∠MBC＋∠NDC＝，BE、DF分别平分四边形的外角∠MBC和∠NDC，则∠CBE＋∠CDH＝（），∠CBE＋β∠DHB＝（），根据＝，则有∠CBE＋∠DHB＝（＋）＝，得到∠CBE＝∠DHB，故可得到BE∥DF．

解：（1）∵∠ABC＋∠ADC＝360°（）＝250°，

∴∠MBC＋∠NDC＝180°∠ABC＋180°∠ADC＝360°-（∠ABC＋∠ADC）=＝110°．

故答案为：110；

（2）．理由如下：如解图①，连接BD，

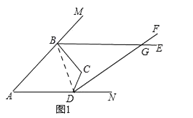
由（1）知，，

、分别平分四边形的外角和，

∴，

．

在△BCD中，∠BDC＋∠CBD＝180°∠BCD＝180°，

在△BDG中，∠GBD＋∠GDB＋∠BGD＝180°，

∴∠CBG＋∠CBD＋∠CDG＋∠BDC＋∠BGD＝180°，

∴（∠CBG＋∠CDG）＋（∠BDC＋∠CBD）＋∠BGD＝180°，

∴（）＋180°＋25°＝180°，

整理得；

（3）．理由如下，如解图②所示，延长交于点，

由（1）、（2）可知，，

．

，

，

．

，

，

，

．