题目内容
在数学里,我们规定:a-n=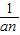 (a≠O).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了.例如a2•a-3=a2+(-3)=a-1=
(a≠O).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了.例如a2•a-3=a2+(-3)=a-1=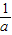 .数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+
.数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+ i=
i= i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6•0.5i=3i; 2i•3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±
i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6•0.5i=3i; 2i•3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±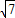 i.…数的不断发展进一步证实,这种规定是合理的.
i.…数的不断发展进一步证实,这种规定是合理的.(1)想一想,作这样的规定有什么好处?
(2)试用配方法求一元二次方程x2+x+1=0的非实数解:
(3)你认为,在学习中,当面临一个新的挑战时,我们应如何面对?
【答案】分析:(1)通过阅读分析,可以看出有了这种规定可以解决在实数范围内不能解决的问题,负数的平方的问题.
(2)先将原式配方后变为(x+ )2=-
)2=- ,再将x+
,再将x+ 当作一个整体按照条件中的方法就可以求出其值.
当作一个整体按照条件中的方法就可以求出其值.
(3)是一个结论开方性试题,要体现一种不怕困难的精神,要求学生在学习中勇于探索.
解答:解:(1)由题意可以看出这样规定有利于经负数的平方运算.
(2)原方程变形为:(x+ )2=-
)2=- ,
,
∴x+ =±
=± i,
i,
∴x1= i-
i- ,x2=-
,x2=- i-
i- .
.
(3)我们在学习中遇到新的挑战时,要大胆探索,运用已有的知识总结出新的结论.
点评:本题考查了一元二次方程的解法及运用,在解答中要求学生具有较强的阅读能力和分析能力,解决现实生活中的实际问题.
(2)先将原式配方后变为(x+
 )2=-
)2=- ,再将x+
,再将x+ 当作一个整体按照条件中的方法就可以求出其值.
当作一个整体按照条件中的方法就可以求出其值.(3)是一个结论开方性试题,要体现一种不怕困难的精神,要求学生在学习中勇于探索.
解答:解:(1)由题意可以看出这样规定有利于经负数的平方运算.
(2)原方程变形为:(x+
 )2=-
)2=- ,
,∴x+
 =±
=± i,
i,∴x1=
 i-
i- ,x2=-
,x2=- i-
i- .
.(3)我们在学习中遇到新的挑战时,要大胆探索,运用已有的知识总结出新的结论.
点评:本题考查了一元二次方程的解法及运用,在解答中要求学生具有较强的阅读能力和分析能力,解决现实生活中的实际问题.

练习册系列答案
相关题目
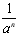 (a≠0).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了。例如a2·a-3=a2+(-3)=a-1=
(a≠0).无论从仿照同底数幂的除法公式来分析,还是仿照分式的约分来分析,这种规定都是合理的.正是有了这种规定,指数的范围由非负数扩大到全体整数,概念的扩充与完善使我们解决问题的路更宽了。例如a2·a-3=a2+(-3)=a-1=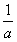 ,数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+
,数的发展经历了漫长的过程,其实人们早就发现了非实数的数.人们规定:i2=-1,这里数i类似于实数单位1,它的运算法则与实数运算法则完全类似:2i+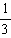 i=
i=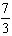 i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6·0.5i=3i;2i·3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±
i(注意:由于非实数与实数单位不同,因此像2+i之类的运算便无法继续进行,2+i就是一个非实数的数),6·0.5i=3i;2i·3i=6i2=-6;(3i)2=-9;-4的平方根为±2i;如果x2=-7,那么x=±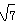 i.…数的不断发展进一步证实,这种规定是合理的.试用配方法求一元二次方程x2+x+1=0的非实数解:
i.…数的不断发展进一步证实,这种规定是合理的.试用配方法求一元二次方程x2+x+1=0的非实数解: