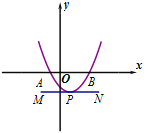��Ŀ����
����Ŀ����һ��ֱ�����ǰ���ͼ�ٰڷţ��ܹ����ֵ���ֱ�����ǰ�ABC��б���뺬30���ǵ�ֱ�����ǰ�DEF�ij�ֱ�DZ�DE�غϣ�DF=8��
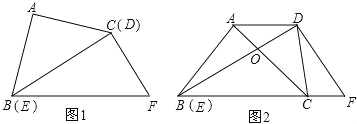
��1����P��BC�ϵ�һ�����㣬��PA=DFʱ�����ʱ��PAB�Ķ�����
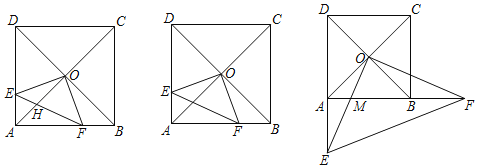
��2����ͼ���еĵ���ֱ�����ǰ�ABC�Ƶ�B˳ʱ����ת30������C����BF�ϣ�AC��BD���ڵ�O������CD����ͼ�ڣ�
��̽����CDO����״����˵�����ɣ�
����ͼ���У���P��BC���е㣬����FP��������ֱ�����ǰ�ABC�Ƶ�B˳ʱ����ת������ת����= ʱ��FP����������ֵΪ ��ֱ��д���𰸼��ɣ���
���𰸡���1��![]() ��
��![]() ����2���ټ���⣻��
����2���ټ���⣻��![]() ��
��![]() .
.
��������
��1����![]() ��BC�ڵ�H���ɵ������������ߺ�һ��ֱ��������б�����ߵ����ʿɵ�
��BC�ڵ�H���ɵ������������ߺ�һ��ֱ��������б�����ߵ����ʿɵ�![]() ����
����![]() �н�ֱ�������ο�֪BC������֪AH��������
�н�ֱ�������ο�֪BC������֪AH��������![]() �н�ֱ�������ο�֪
�н�ֱ�������ο�֪![]() ���ֵ�P��
���ֵ�P��![]() λ�ú���
λ�ú���![]() λ��2�������⼴�ɣ�
λ��2�������⼴�ɣ�
��2�������õ���������������ȼ���������ǵ����ʿ����![]() ����֪��CDOΪ���������Σ�
����֪��CDOΪ���������Σ�
���ɵ�P��BC���е㣬FP�������֪��F��B��P��ͬһ��ֱ���ϣ�����P��FB���ӳ����ϣ���֪��ת��![]() �����BP��BF�ij�����Ӽ�ΪFP��.
�����BP��BF�ij�����Ӽ�ΪFP��.
�⣺��1����ͼ����![]() ��BC�ڵ�H��
��BC�ڵ�H��

![]() Ϊ����ֱ��������
Ϊ����ֱ��������
![]()
![]()
![]()
![]()
![]()
��![]() ʱ��
ʱ��![]()
![]()
����P��![]() λ��ʱ��
λ��ʱ��
![]() ��
��![]()
![]() ��
��
����P��![]() λ��ʱ��
λ��ʱ��
![]() ��
��![]()
![]()
![]()
![]()
������������PAB�Ķ���Ϊ![]() ��
��![]() ��
��
��2������CDO����������.
![]()
![]() ����
����![]()
![]()
![]()
![]()
![]()
������CDO����������
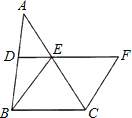
��![]() ��P��BC���е㣬FP����������F��B��P��ͬһ��ֱ���ϣ�����P��FB���ӳ����ϣ���ͼ��ʾ��
��P��BC���е㣬FP����������F��B��P��ͬһ��ֱ���ϣ�����P��FB���ӳ����ϣ���ͼ��ʾ��
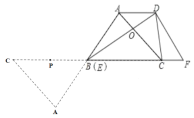
![]() ����ת��
����ת��![]()
![]()
![]()
![]() ��P
��P![]()
![]()
��![]() ��
�У�
![]()
![]()
![]()
���Ե���ת��![]() ʱ��FP����������ֵΪ
ʱ��FP����������ֵΪ![]() .
.