题目内容
1. 如图,A、B分别为x轴、y轴上的两点,⊙G是△AOB的内切圆,切点分别为D、E、F,其半径为r,△AOB的两条直角边OB、OA分别为a,b,且a,b是一元一次方程x2-14x+m=0的两个根,AB=c.
如图,A、B分别为x轴、y轴上的两点,⊙G是△AOB的内切圆,切点分别为D、E、F,其半径为r,△AOB的两条直角边OB、OA分别为a,b,且a,b是一元一次方程x2-14x+m=0的两个根,AB=c.(1)当⊙G的面积为4π时,过D、E两点直线的解析式为y=-x+2;
(2)当a:b=2:5时,求a、b的值;
(3)确定c与r的关系,确定c与m的关系.
分析 (1)如图,连接EG、DG,首先证明四边形OEGD是正方形,求出D、E坐标,利用待定系数法即可解决问题.
(2)利用根与系数关系可知a+b=14,又a:b=2:5,解方程组即可解决.
(3)根据切线长定理、勾股定理以及根与系数关系即可解决问题.
解答 解:(1)如图,连接EG、DG.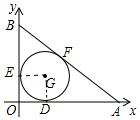
∵D、E是切点,
∴∠OEG=∠ODG=∠EOD=90°,
∴四边形OEGD是矩形,
∵GE=GD,
∴四边形OEGD是正方形,
∴OE=OD=GE=GD,
∵⊙G的面积为4π,
∴πr2=4π,
∵r>0,
∴r=2,
∴OE=OD=2,
∴E(0,2),D(2,0),
设直线DE的解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=2}\\{2k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
∴直线DE的解析式为y=-x+2.
故答案为y=-x+2.
(2)a,b是一元一次方程x2-14x+m=0的两个根,
∴a+b=14,又a:b=2:5,
∴a=4,b=10.
(3)由切线长定理可知,BE=BF=a-r,AD=AF=b-r,
∵c=AB=BF+AF=a+b-2r,a+b=14,
∴c=14-2r.
∵c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{(a+b)^{2}-2ab}$,a+b=14,ab=m,
∴c=$\sqrt{196-2m}$.
点评 本题考查圆的综合题、一次函数的应用、待定系数法、三角形内切圆、一元二次方程的根与系数关系、切线长定理、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中考压轴题.

练习册系列答案
相关题目
11.下面说法中正确的是( )
| A. | 真分数小于1,假分数大于1 | B. | 小于1的真分数有4个 | ||
| C. | 最简分数的分子和分母没有公约数 | D. | 假分数的倒数不一定是真分数 |
6.小明接到一项任务:要到文具店购买笔记本、圆珠笔和钢笔共30件,各种商品的价格如下表:
(1)笔记本和圆珠笔的总件数不小于钢笔的支数,则小明至多能买几支钢笔?
(2)若小明仅有100元,要完成任务至多能买几支钢笔?
| 物品 | 笔记本 | 圆珠笔 | 钢笔 |
| 单价(元) | 2 | 2 | 5 |
(2)若小明仅有100元,要完成任务至多能买几支钢笔?
5.一件衣服提高价格25%后发现销路不是很好,欲恢复原价,则应降价( )
| A. | 40% | B. | 20% | C. | 25% | D. | 15% |
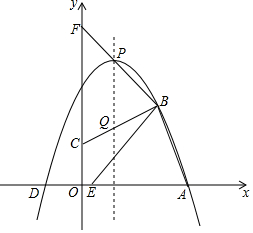 如图,二次函数y=ax2+bxc的图象经过A(4,0),D(-1,0)和B(3,3)三,.顶点为点P.作BC⊥BA交y轴于C,交对称轴于Q,将∠CBA绕点B顺时针旋转,∠CBA的两边分别交x轴、y轴于点E、F.设点E的坐标为(m,0).
如图,二次函数y=ax2+bxc的图象经过A(4,0),D(-1,0)和B(3,3)三,.顶点为点P.作BC⊥BA交y轴于C,交对称轴于Q,将∠CBA绕点B顺时针旋转,∠CBA的两边分别交x轴、y轴于点E、F.设点E的坐标为(m,0).