题目内容
 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF.(1)这两个三角形相似吗?为什么?
(2)求∠A的度数;
(3)在右边的网格再画一个三角形,使它与△ABC相似,并求出其相似比.
分析:(1)根据勾股定理列式求出AB、AC、BC、DE、DF、EF的长度,然后根据三边对应成比例,两三角形相似解答;
(2)取AC的中点O,连接BO,根据网格结构可以判断∠ABO=90°,△ABO是等腰直角三角形,即可得解;
(3)把△ABC三边扩大
倍,然后利用网格结构作出即可.
(2)取AC的中点O,连接BO,根据网格结构可以判断∠ABO=90°,△ABO是等腰直角三角形,即可得解;
(3)把△ABC三边扩大
| 2 |
解答: 解:(1)AB=
解:(1)AB=
=
,
AC=
=2
,
BC=5,
DE=1,
DF=
=
,
EF=
=2
,
∵
=
=
=
,
∴△ABC∽△DEF;
(2)如图,取AC的中点O,连接BO,
则△ABO是等腰直角三角形,
∴∠A=45°;
(3)如图,△A′B′C′与△ABC相似,它们的相似比是
.
 解:(1)AB=
解:(1)AB=| 12+22 |
| 5 |
AC=
| 22+62 |
| 10 |
BC=5,
DE=1,
DF=
| 12+22 |
| 5 |
EF=
| 22+22 |
| 2 |
∵
| AB |
| DE |
| AC |
| EF |
| BC |
| DF |
| 5 |
∴△ABC∽△DEF;
(2)如图,取AC的中点O,连接BO,
则△ABO是等腰直角三角形,
∴∠A=45°;
(3)如图,△A′B′C′与△ABC相似,它们的相似比是
| 2 |
点评:本题考查了利用相似变换作图,熟练掌握相似三角形的判定与性质,网格结构的特点是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
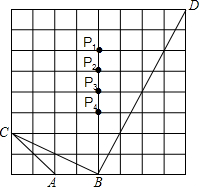 如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.| A、P1 | B、P2 | C、P3 | D、P4 |
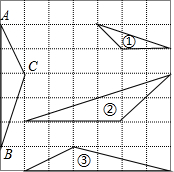 如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有
如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有 如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是
如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF. 作图计算题.
作图计算题.