题目内容
数学习题课上,数学老师布置了这样一道练习:四边形ABCD中,有下列三个论断:①AB∥DC;②AD=BC;③∠A=∠C;
请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.
李梅同学写出了命题1:已知四边形ABCD中,AB∥DC,∠A=∠C,则AD=BC.
王华同学写出了命题2:已知四边形ABCD中,AB∥DC,AD=BC,则∠A=∠C.
你认为命题1和命题2都正确吗?若正确,请加以证明;若不正确,请举反例说明理由.
解:(1)命题1正确.
证明:如图,连接BD
∵AB∥DC,
∴∠ABD=∠CDB,
在△ABD和△CDB中,

∴△ABD≌△CDB,
∴AD=BC;
(2)当四边形ABCD为等腰梯形时,该命题不正确,如图:

分析:(1)根据题意画出图形,再根据已知和三角形的判定证出△ABD≌CDB,即可得出正确答案.
(2)根据题意画出图形,根据等腰梯形的性质得出∠A≠∠C,从而得出命题不正确.
点评:此题考查了命题与定理,解题的关键是画出图形,再根据三角形的判定和等腰梯形的性质得出命题的正确性.
证明:如图,连接BD
∵AB∥DC,

∴∠ABD=∠CDB,
在△ABD和△CDB中,

∴△ABD≌△CDB,
∴AD=BC;
(2)当四边形ABCD为等腰梯形时,该命题不正确,如图:

分析:(1)根据题意画出图形,再根据已知和三角形的判定证出△ABD≌CDB,即可得出正确答案.
(2)根据题意画出图形,根据等腰梯形的性质得出∠A≠∠C,从而得出命题不正确.
点评:此题考查了命题与定理,解题的关键是画出图形,再根据三角形的判定和等腰梯形的性质得出命题的正确性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
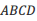 中,有下列三个论断:①
中,有下列三个论断:①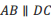 ;②
;②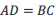 ;③
;③ ;请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.李梅同学写出了命题1:已知四边形
;请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.李梅同学写出了命题1:已知四边形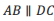 ,
, 中,有下列三个论断:①
中,有下列三个论断:① ;②
;② ;③
;③ ;请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.李梅同学写出了命题1:已知四边形
;请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.李梅同学写出了命题1:已知四边形 ,
, 中,有下列三个论断:①
中,有下列三个论断:① ;②
;② ;③
;③ ;请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.李梅同学写出了命题1:已知四边形
;请以其中两个论断作为题设,另一个论断作为结论,写出一个你认为正确的命题.李梅同学写出了命题1:已知四边形 ,
,